
ĄžĚâÄżĄżÄłš¤łĚśÓš˛ÓĐ500ČËŁŹŇŞ˝¨ÔěŇťśÎ6000Ă׾ĸßËŮšŤÂˇŁŹš¤łĚĐčŇŞ°Ń500ČˡֳÉÁ˝×飏ź××éľÄČÎÎńĘÇÍęłÉŇťśÎ4000Ă׾ÄČíÍÁľŘ´řŁŹŇŇ×éľÄČÎÎńĘÇÍęłÉĘŁĎÂľÄ2000Ă׾ÄÓ˛ÍÁľŘ´řŁŹžÝ˛âË㣏ČíĄ˘Ó˛ÍÁľŘĂżĂ׾̤łĚÁżĘÇ30š¤Ł¨š¤ÎŞźĆÁżľĽÎťŁŠşÍ40š¤.
Ł¨1ŁŠČôĆ˝žůˇÖĹäÁ˝×éľÄČËĘýŁŹˇÖąđźĆËăÁ˝×éÍꚤľÄĘąźäŁŹ˛˘Çółö´ËʹȍśÓľÄÖţ¡š¤ĆÚŁť
Ł¨2ŁŠČçşÎˇÖĹäÁ˝×éľÄČËĘýťáĘšľĂČŤśÓľÄÖţ¡š¤ĆÚ×îśĚŁż
Ąž´đ°¸ĄżŁ¨1ŁŠźű˝âÎöŁ¨2ŁŠÓ˛ÍÁŁŹČíÍÁľÄČËĘýˇÖąđˇÖĹäÎŞ275ŁŹ225ĘąŁŹČŤśÓš¤ĆÚ×îśĚŁŹÎŞ437ŁŽ
Ąž˝âÎöĄż
Ł¨1ŁŠĆ˝žůˇÖĹäÁ˝×éľÄČËĘý¸÷ÎŞ250ČËŁŹÁ˝×éÍꚤľÄĘąźäˇÖąđÎŞŁş![]() ŁŹ
ŁŹ![]() ŁŽżÉľĂ´ËʹȍśÓľÄÖţ¡š¤ĆÚŁŽ
ŁŽżÉľĂ´ËʹȍśÓľÄÖţ¡š¤ĆÚŁŽ
Ł¨2ŁŠźŮÉčˇÖĹäÁ˝×éľÄČËĘýˇÖąđÎŞxŁŹ500ŠxŁŽżÉľĂÁ˝×éÍꚤľÄĘąźäˇÖąđÎŞŁş![]() ŁŹ
ŁŹ![]() ŁŽżÉľĂÁ˝×éÍꚤľÄĘąźäşÍ
ŁŽżÉľĂÁ˝×éÍꚤľÄĘąźäşÍ![]() 40000
40000![]() .0ŁźxŁź500ŁŽÁîfŁ¨xŁŠ
.0ŁźxŁź500ŁŽÁîfŁ¨xŁŠ![]() ŁŹ0ŁźxŁź500ŁŽŔűÓĂľźĘýŃĐžżĆ侼ľ÷ĐÔźŤÖľÓë×îÖľź´żÉľĂłöŁŽ
ŁŹ0ŁźxŁź500ŁŽŔűÓĂľźĘýŃĐžżĆ侼ľ÷ĐÔźŤÖľÓë×îÖľź´żÉľĂłöŁŽ
Ł¨1ŁŠĆ˝žůˇÖĹäÁ˝×éľÄČËĘý¸÷ÎŞ250ČËŁŹÁ˝×éÍꚤľÄĘąźäˇÖąđÎŞŁş![]() 480ŁŹ
480ŁŹ![]() 320ŁŽ
320ŁŽ
Ąŕ´ËʹȍśÓľÄÖţ¡š¤ĆÚÎŞ480ŁŽ
ĄŕÓ˛ÍÁ480ŁŹČíÍÁ320ŁŹČŤśÓš¤ĆÚ480Łť
Ł¨2ŁŠźŮÉčˇÖĹäÁ˝×éľÄČËĘýˇÖąđÎŞxŁŹ500ŠxŁŽ
ÔňŁşÁ˝×éÍꚤľÄĘąźäˇÖąđÎŞŁş![]() ŁŹ
ŁŹ![]() ŁŽ
ŁŽ
ĄŕÁ˝×éÍꚤľÄĘąźäşÍ![]() 40000
40000![]() .0ŁźxŁź500ŁŽ
.0ŁźxŁź500ŁŽ
ÁîfŁ¨xŁŠ![]() ŁŹ0ŁźxŁź500ŁŽ
ŁŹ0ŁźxŁź500ŁŽ
ĄŕfĄäŁ¨xŁŠ![]() 0ŁŹ
0ŁŹ
˝âľĂxŁ˝1500Š500![]() 275ŁŽ
275ŁŽ
ĄŕČŤśÓľÄÖţ¡š¤ĆÚÎŞ![]() 437ŁŽ
437ŁŽ
Áí˝âŁşy![]() ŁŹ0ŁźxŁź500ŁŽ
ŁŹ0ŁźxŁź500ŁŽ
Ôňy![]() Ł¨x+500ŠxŁŠŁ¨
Ł¨x+500ŠxŁŠŁ¨![]() ŁŠ
ŁŠ![]() Ł¨5
Ł¨5![]() ŁŠ
ŁŠ![]() Ł¨5+2
Ł¨5+2![]() ŁŠŁŹ
ŁŠŁŹ
ľąÇŇ˝öľąxŁ˝1500Š500![]() 275ʹȥľČşĹŁŽ
275ʹȥľČşĹŁŽ
ĄŕÓ˛ÍÁŁŹČíÍÁľÄČËĘýˇÖąđˇÖĹäÎŞ275ŁŹ225ĘąŁŹČŤśÓš¤ĆÚ×îśĚŁŹÎŞ437ŁŽ



| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹÔÚÖąČýŔâÖů![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹľăEŁŹFˇÖąđÔÚ
ŁŹľăEŁŹFˇÖąđÔÚ![]() ŁŹ
ŁŹ![]() ŁŹÇŇ
ŁŹÇŇ![]() ŁŹ
ŁŹ![]() .Éč
.Éč![]() .
.
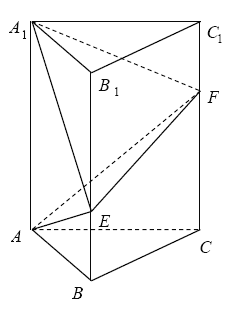
Ł¨1ŁŠľą![]() ĘąŁŹÇóŇěĂćÖąĎß
ĘąŁŹÇóŇěĂćÖąĎß![]() Óë
Óë![]() ËůłÉ˝ÇľÄ´óĐĄŁť
ËůłÉ˝ÇľÄ´óĐĄŁť
Ł¨2ŁŠľąĆ˝Ăć![]() Ć˝Ăć
Ć˝Ăć![]() ĘąŁŹÇó
ĘąŁŹÇó![]() ľÄÖľ.
ľÄÖľ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
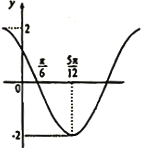
ĄžĚâÄżĄżČôşŻĘý![]() ľÄľźşŻĘý
ľÄľźşŻĘý![]() ŁŹ
ŁŹ![]() ľÄ˛żˇÖÍźĎóČçÍźËůĘžŁŹ
ľÄ˛żˇÖÍźĎóČçÍźËůĘžŁŹ![]() ŁŹľą
ŁŹľą![]() ŁŹ
ŁŹ![]() ĘąŁŹÔň
ĘąŁŹÔň![]() ľÄ×î´ó־Ϊ_________.
ľÄ×î´ó־Ϊ_________.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłşćąşľęźÓš¤Ňť¸öłÉąžÎŞ60ÔŞľÄľ°¸âŁŹČťşóŇÔĂż¸ö120ÔŞľÄźŰ¸ńłöĘŰŁŹČçšűľąĚěÂô˛ťÍ꣏ʣĎÂľÄŐâÖÖľ°¸â×÷˛ÍłřŔŹťř´ŚŔí.
Ł¨1ŁŠČôşćąşľęŇťĚěźÓš¤16¸öŐâÖÖľ°¸âŁŹÇóľąĚěľÄŔűČó![]() Ł¨ľĽÎťŁşÔŞŁŠšŘÓÚľąĚěĐčÇóÁż
Ł¨ľĽÎťŁşÔŞŁŠšŘÓÚľąĚěĐčÇóÁż![]() Ł¨ľĽÎťŁş¸öŁŹ
Ł¨ľĽÎťŁş¸öŁŹ![]() ŁŠľÄşŻĘý˝âÎöĘ˝Łť
ŁŠľÄşŻĘý˝âÎöĘ˝Łť
Ł¨2ŁŠÎŞÁË˝â¸ĂÖÖľ°¸âľÄĘĐłĄĐčÇóÇéżöÓëĐÔeĘǡńÓКأŹËćťúÍłźĆÁË100Č˾ĚşÂňÇéżöŁŹľĂČçĎÂÁĐÁŞąíŁş
ÄĐ | ĹŽ | şĎźĆ | |
šşÂň | 15 | 35 | 50 |
˛ťšşÂň | 6 | 44 | 50 |
şĎźĆ | 21 | 79 | 100 |
ÎĘŁşÄܡńÓĐ![]() ľÄ°ŃÎŐČĎÎŞĘǡńšşÂňľ°¸âÓëĐÔeÓКأż
ľÄ°ŃÎŐČĎÎŞĘǡńšşÂňľ°¸âÓëĐÔeÓКأż
¸˝Łş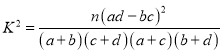
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżĎÂÁĐşŻĘýÔÚĆ䜨ŇĺÓňÉĎźČĘÇĆ溯ĘýŁŹÓÖĘÇÔöşŻĘýľÄĘÇŁ¨ ŁŠ
A.![]() B.
B.![]()
C.![]() D.
D.![]()
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹŇŃÖŞËÄŔâלPŁABCDÖĐŁŹľ×ĂćABCDĘÇÖą˝ÇĚÝĐÎŁŹAD//BCŁŹBCŁ˝2ADŁŹADĄÍCDŁŹPDĄÍĆ˝ĂćABCDŁŹEÎŞPBľÄÖĐľă.
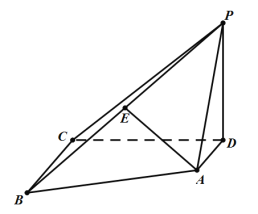
(1)ÇóÖ¤ŁşAE//Ć˝ĂćPDCŁť
(2)ČôBCŁ˝CDŁ˝PDŁŹÇóÖąĎßACÓëĆ˝ĂćPBCËůłÉ˝ÇľÄÓŕĎŇÖľ.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżşŻĘý![]() .
.
Ł¨1ŁŠ¸ůžÝ![]() ˛ťÍŹČĄÖľŁŹĚÖÂŰşŻĘý
˛ťÍŹČĄÖľŁŹĚÖÂŰşŻĘý![]() ľÄĆćĹźĐÔŁť
ľÄĆćĹźĐÔŁť
Ł¨2ŁŠČô![]() ŁŹśÔÓÚČÎŇâľÄ
ŁŹśÔÓÚČÎŇâľÄ![]() ŁŹ˛ťľČĘ˝
ŁŹ˛ťľČĘ˝![]() şăłÉÁ˘ŁŹÇóĘľĘý
şăłÉÁ˘ŁŹÇóĘľĘý![]() ľÄČĄÖľˇśÎ§Łť
ľÄČĄÖľˇśÎ§Łť
Ł¨3ŁŠČôŇŃÖŞ![]() ŁŹ
ŁŹ![]() . É躯Ęý
. É躯Ęý![]() ŁŹ
ŁŹ![]() ŁŹ´ćÔÚ
ŁŹ´ćÔÚ![]() Ą˘
Ą˘![]() ŁŹĘšľĂ
ŁŹĘšľĂ![]() ŁŹÇóĘľĘý
ŁŹÇóĘľĘý![]() ľÄČĄÖľˇśÎ§.
ľÄČĄÖľˇśÎ§.
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹÔ˛×śľÄľ×Ăć°ëžś![]() ŁŹ¸ß
ŁŹ¸ß![]() ŁŹľă
ŁŹľă![]() ĘÇľ×ĂćÖąžś
ĘÇľ×ĂćÖąžś![]() ËůśÔťĄľÄÖо㣏ľă
ËůśÔťĄľÄÖо㣏ľă![]() ĘÇĸĎß
ĘÇĸĎß![]() ľÄÖĐľă.
ľÄÖĐľă.
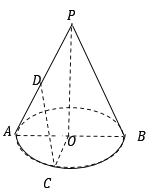
Ł¨1ŁŠÇóԲלľÄ˛ŕĂćťýşÍĚĺťýŁť
Ł¨2ŁŠÇóŇěĂćÖąĎß![]() Óë
Óë![]() ËůłÉ˝ÇľÄ´óĐĄ.Ł¨˝ášűÓá´Čý˝ÇşŻĘýąíĘžŁŠ
ËůłÉ˝ÇľÄ´óĐĄ.Ł¨˝ášűÓá´Čý˝ÇşŻĘýąíĘžŁŠ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÄłĘĄĆŐͨ¸ßÖĐѧҾˎƽżźĘԳɟ¨°´ČËĘýËůŐźąČŔýŇŔ´ÎÓɸ߾˝ľÍˇÖÎŞ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() Îĺ¸öľČźśŁŹ
Îĺ¸öľČźśŁŹ![]() ľČźś
ľČźś![]() ŁŹ
ŁŹ![]() ľČźś
ľČźś![]() ŁŹ
ŁŹ![]() ľČźś
ľČźś![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ľČźśš˛
ľČźśš˛![]() .ĆäÖĐ
.ĆäÖĐ![]() ľČźśÎŞ˛ťşĎ¸ńŁŹÔÔňÉĎąČŔý˛ťłŹšý
ľČźśÎŞ˛ťşĎ¸ńŁŹÔÔňÉĎąČŔý˛ťłŹšý![]() .¸ĂʥijУ¸ßśţÄꟜѧÉúśź˛ÎźÓѧҾˎƽżźĘÔŁŹĎČ´ÓÖĐËćťúłéČĄÁ˲żˇÖѧÉúľÄżźĘԳɟ¨˝řĐĐÍłźĆŁŹÍłźĆ˝ášűČçÍźËůĘž.Čô¸ĂĐŁ¸ßśţÄęźśš˛ÓĐ1000ĂűѧÉúŁŹÔňšŔźĆ¸ĂÄęźśÄĂľ˝
.¸ĂʥijУ¸ßśţÄꟜѧÉúśź˛ÎźÓѧҾˎƽżźĘÔŁŹĎČ´ÓÖĐËćťúłéČĄÁ˲żˇÖѧÉúľÄżźĘԳɟ¨˝řĐĐÍłźĆŁŹÍłźĆ˝ášűČçÍźËůĘž.Čô¸ĂĐŁ¸ßśţÄęźśš˛ÓĐ1000ĂűѧÉúŁŹÔňšŔźĆ¸ĂÄęźśÄĂľ˝![]() źśź°ŇÔÉĎźśąđľÄѧÉúČËĘýÓĐŁ¨ ŁŠ
źśź°ŇÔÉĎźśąđľÄѧÉúČËĘýÓĐŁ¨ ŁŠ
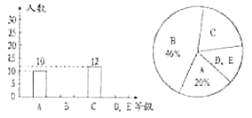
A.45ČËB.660ČËC.880ČËD.900ČË
˛éż´´đ°¸şÍ˝âÎö>>
°ŮśČÖÂĐĹ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com