
分析 (1)根据向量的模的计算和同角三角函数的关系即可求出;
(2)根据向量的坐标运算和模的计算和三角函数的性质即可求出.
解答 解:(1)向量$\overrightarrow{a}$=(cos2x,sin2x),
∴|$\overrightarrow{a}$|=$\sqrt{co{s}^{2}2x+si{n}^{2}2x}$=1,
(2)$\overrightarrow{c}$=$\overrightarrow{a}$-$\overrightarrow{b}$=(cos2x-cosa,sin2x-sinα),
∴|$\overrightarrow{c}$|2=(cos2x-cosa)2+(sin2x-sinα)2=2-2(cos2xcosα+sin2xsinα)=2-2cos(2x-α),
∵x∈R,α∈[0,2π],
∴2x-α∈R,
∴-1≤cos(2x+α)≤1,
∴0≤2-2cos(2x+α)≤4,
∴0≤|$\overrightarrow{c}$|≤2,
∴|$\overrightarrow{c}$|的取值范围是[0,2].
故答案为:(1)1,(2)[0,2].
点评 本题考查了向量模的计算和两角差的余弦正弦公式、余弦函数的性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧(¬q) | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
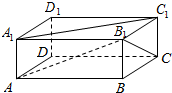 如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.
如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com