已知f(x)=ax5-bx3+c(a>0)在x=±1处有极值,且极大值为4,极小值为0,试确定a、b、c的值.
分析:先求函数的导数,根据题意f′(x)=0应有根x=±1,可得一个关系式,再借助两个极值建立两个等量关系,解三元一次方程组即可.
解答:解:已知f(x)=ax
5-bx
3+c,
所以f′(x)=5ax
4-3bx
2=x
2(5ax
2-3b).
根据题意f′(x)=0应有根x=±1,
故5a=3b.
所以f′(x)=5ax
2(x
2-1).
因a>0时,列表:
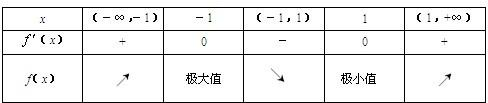
由上表可见
| | 4=f(-1)=-a+b+c① | | 0=f(1)=a-b+c.② |
| |
①+②得c=2,
①-②得b=a+2.
又5a=3b,所以a=3,b=5,c=2.
点评:本题主要考查了利用导数研究函数的极值,通过极值求解系数,属于中档题.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案