
|
| y |
| x |
| ||
| 3 |
| ||
| 3 |
|
| y |
| x |
 解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)
解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)| y |
| x |
| 3 |
| 2 |
| ||
| 2 |
| y |
| x |
| ||
| 3 |
| y |
| x |
| y |
| x |
| ||
| 3 |
| ||
| 3 |


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
| 1 |
| 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+| 2π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
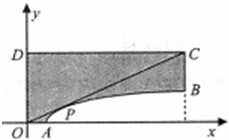 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届陕西省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
设 为坐标原点,
为坐标原点, ,
,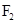 是双曲线
是双曲线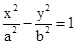 (a>0,b>0)的焦点,若在双曲
(a>0,b>0)的焦点,若在双曲
线上存在点P,满足∠ P
P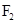 =60°,∣OP∣=
=60°,∣OP∣= ,则该双曲线的渐近线方程为(
)
,则该双曲线的渐近线方程为(
)
A.x± y=0
B.
y=0
B. x±y=0
x±y=0
C. x± =0 D.
=0 D. ±y=0
±y=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com