【题目】如图，长方体ABCD﹣A1B1C1D1中，AA1=AB=2，AD=1点E，F，G分别是DD1 ， AB，CC1的中点，则异面直线A1E与GF所成的角是（ ）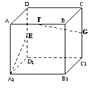 
A.90°
B.60°
C.45°
D.30°
【答案】A
【解析】解：由题意：ABCD﹣A1B1C1D1是长方体，E，F，G分别是DD1 ， AB，CC1的中点，连接B1G， ∵A1E∥B1G，
∴∠FGB1为异面直线A1E与GF所成的角．
连接FB1 ， 
在三角形FB1G中，AA1=AB=2，AD=1，
B1F= 
= 
B1G= 
= 
，
FG= 
= 
，
B1F2=B1G2+FG2 ．
∴∠FGB1=90°，
即异面直线A1E与GF所成的角为90°．
故选A．
异面直线所成的角通过平移相交，找到平面角，转化为平面三角形的角求解，由题意：E，F，G分别是DD1 ， AB，CC1的中点，连接B1G，FB1 ， 那么∠FGB1就是异面直线A1E与GF所成的角．
科目：高中数学 来源： 题型：
【题目】若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数，指定0，1，2，3表示没有击中目标，4，5，6，7，8，9表示击中目标，以4个随机数为一组，代表射击4次的结果，经随机模拟产生了20组如下的随机数：
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为_________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣1．
（1）求f（3）+f（﹣1）；
（2）求f（x）在R上的解析式；
（3）求不等式﹣7≤f（x）≤3的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
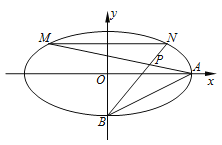
【题目】如图，在平面直角坐标系
中，已知椭圆
过点
， 
， 
分别为椭圆
的右、下顶点，且
．
（1）求椭圆
的方程；
（2）设点
在椭圆
内，满足直线
， 
的斜率乘积为
，且直线
， 
分别交椭圆
于点
， 
．
(i) 若
， 
关于
轴对称，求直线
的斜率；
(ii) 求证： 
的面积与
的面积相等．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2012年，商品价格一度成为社会热点话题，某种新产品投放市场的100天中，前40天价格呈直线上升，由于政府及时采取有效措施，从而使后60天的价格呈直线下降，现统计出其中4天的价格如下表
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格（元） | 23 | 30 | 22 | 7 |
（1）写出价格f（x）关于时间x的函数关系式（x表示投放市场的第x天）；
（2）销售量g（x）与时间x的函数关系： 
（1≤x≤100，且x∈N），则该产品投放市场第几天销售额最高？最高为多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点E，F分别是棱BC，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面AEF，则线段A1P长度的取值范围是 ．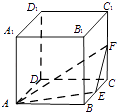 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数F（x）=g（x）+h（x）=ex ， 且g（x），h（x）分别是R上的偶函数和奇函数，若对任意的x∈（0，+∞），不等式g（2x）≥ah（x）恒成立，则实数a的取值范围是（ ）
A.（﹣∞，2 
]
B.（﹣∞，2 ）
C.（﹣∞，2]
D.（﹣∞，2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设{an}是等差数列，下列结论中正确的是（ ）
A.若a1+a2＞0，则a2+a3＞0
B.若a1+a3＜0，则a1+a2＜0
C.若0＜a1＜a2 ， 则a2 
D.若a1＜0，则（a2﹣a1）（a2﹣a3）＞0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
