
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬FКЗЕЧОпПЯCЈєx2=2pyЈЁpЈѕ0Ј©µДЅ№µгЈ¬MКЗЕЧОпПЯCЙПО»УЪµЪТ»ПуПЮДЪµДИОТвТ»µгЈ¬№эMЈ¬FЈ¬OИэµгµДФІµДФІРДОЄQЈ¬µгQµЅЕЧОпПЯCµДЧјПЯµДѕаАлОЄ ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЕЧОпПЯCµД·ЅіМЈ»
ЈЁ2Ј©КЗ·сґжФЪµгMЈ¬К№µГЦ±ПЯMQУлЕЧОпПЯCПаЗРУЪµгMЈїИфґжФЪЈ¬ЗуіцµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЛµГчАнУЙЈ»
ЈЁ3Ј©ИфµгMµДєбЧш±кОЄ ![]() Ј¬Ц±ПЯlЈєy=kx+
Ј¬Ц±ПЯlЈєy=kx+ ![]() УлЕЧОпПЯCУРБЅёцІ»Н¬µДЅ»µгAЈ¬BЈ¬lУлФІQУРБЅёцІ»Н¬µДЅ»µгDЈ¬EЈ¬Зуµ±
УлЕЧОпПЯCУРБЅёцІ»Н¬µДЅ»µгAЈ¬BЈ¬lУлФІQУРБЅёцІ»Н¬µДЅ»µгDЈ¬EЈ¬Зуµ± ![]() ЎЬkЎЬ2К±Ј¬|AB|2+|DE|2µДЧоРЎЦµЈ®
ЎЬkЎЬ2К±Ј¬|AB|2+|DE|2µДЧоРЎЦµЈ®
Ўѕґр°ёЎї
ЈЁ1Ј©ЅвЈєУЙМвТвїЙЦЄFЈЁ0Ј¬ ![]() Ј©Ј¬ФІРДQФЪПЯ¶ОOFЖЅ·ЦПЯy=
Ј©Ј¬ФІРДQФЪПЯ¶ОOFЖЅ·ЦПЯy= ![]() ЙПЈ¬
ЙПЈ¬
ТтОЄЕЧОпПЯCµД±кЧј·ЅіМОЄy=©Ѓ ![]() Ј¬
Ј¬
ЛщТФ ![]() Ј¬јґp=1Ј¬
Ј¬јґp=1Ј¬
ТтґЛЕЧОпПЯCµД·ЅіМx2=2yЈ®
ЈЁ2Ј©ЅвЈєјЩЙиґжФЪµгMЈЁx0Ј¬ ![]() Ј©Ј¬ЈЁx0Јѕ0Ј©ВъЧгМхјюЈ¬
Ј©Ј¬ЈЁx0Јѕ0Ј©ВъЧгМхјюЈ¬
ЕЧОпПЯCФЪµгMґ¦µДЗРПЯµДР±ВКОЄ
yЎд ![]() =
= ![]() =x0Ј®
=x0Ј®
Боy= ![]() µГЈ¬
µГЈ¬ ![]() Ј¬
Ј¬
ЛщТФQЈЁ ![]() Ј©Ј¬
Ј©Ј¬
УЦ|QM|=|OQ|Ј¬
№К ![]() Ј¬
Ј¬
ТтґЛ ![]() Ј®УЦx0Јѕ0Ј®
Ј®УЦx0Јѕ0Ј®
ЛщТФx0= ![]() Ј¬ґЛК±MЈЁ
Ј¬ґЛК±MЈЁ ![]() Ј©Ј®
Ј©Ј®
№КґжФЪµгMЈЁ ![]() Ј©Ј¬К№µГЦ±ПЯMQУлЕЧОпПЯCПаЗРУлµгMЈ®
Ј©Ј¬К№µГЦ±ПЯMQУлЕЧОпПЯCПаЗРУлµгMЈ®
ЈЁ3Ј©ЅвЈєµ±x0= ![]() К±Ј¬УЙЈЁўтЈ©µДQЈЁ
К±Ј¬УЙЈЁўтЈ©µДQЈЁ ![]() Ј©Ј¬ЎСQµД°лѕ¶ОЄЈєr=
Ј©Ј¬ЎСQµД°лѕ¶ОЄЈєr= ![]() =
= ![]() Ј®
Ј®
ЛщТФЎСQµД·ЅіМОЄ ![]() Ј®
Ј®
УЙ  Ј¬ХыАнµГ2x2©Ѓ4kx©Ѓ1=0Ј®
Ј¬ХыАнµГ2x2©Ѓ4kx©Ѓ1=0Ј®
ЙиAЈЁx1Ј¬y1Ј©Ј¬BЈЁx2Ј¬y2Ј©Ј¬УЙУЪЎч=16k2+8Јѕ0Ј¬x1+x2=2kЈ¬x1x2=©Ѓ ![]() Ј¬
Ј¬
ЛщТФ|AB|2=ЈЁ1+k2Ј©[ЈЁx1+x2Ј©2©Ѓ4x1x2]=ЈЁ1+k2Ј©ЈЁ4k2+2Ј©Ј®
УЙ 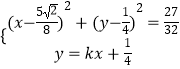 Ј¬ХыАнµГЈЁ1+k2Ј©x2©Ѓ
Ј¬ХыАнµГЈЁ1+k2Ј©x2©Ѓ ![]() Ј¬
Ј¬
ЙиDЈ¬EБЅµгµДЧш±к·Ц±рОЄЈЁx3Ј¬y3Ј©Ј¬ЈЁx4Ј¬y4Ј©Ј¬
УЙУЪЎч= ![]() Јѕ0Ј¬x3+x4=
Јѕ0Ј¬x3+x4= ![]() Ј¬x3x4=
Ј¬x3x4= ![]() Ј®
Ј®
ЛщТФ|DE|2=ЈЁ1+k2Ј©[ЈЁx3+x4Ј©2©Ѓ4x3x4]= ![]() Ј¬
Ј¬
ТтґЛ|AB|2+|DE|2=ЈЁ1+k2Ј©ЈЁ4k2+2Ј©+ ![]() Ј¬
Ј¬
Бо1+k2=tЈ¬УЙУЪЎч=16k2+8Јѕ0 ![]() Ј¬
Ј¬
![]() ЎЬkЎЬ2Ј¬ЎаtЎЭ
ЎЬkЎЬ2Ј¬ЎаtЎЭ ![]()
Фт ![]() Ј¬
Ј¬
ЛщТФ|AB|2+|DE|2=tЈЁ4t©Ѓ2Ј©+ ![]() =4t2©Ѓ2t+
=4t2©Ѓ2t+ ![]() Ј¬
Ј¬
ЙиgЈЁtЈ©=4t2©Ѓ2t+ ![]() Ј¬t
Ј¬t ![]() Ј¬ТтОЄgЎдЈЁtЈ©=8t©Ѓ2©Ѓ
Ј¬ТтОЄgЎдЈЁtЈ©=8t©Ѓ2©Ѓ ![]() Ј¬
Ј¬
ЛщТФµ±t ![]() Ј¬gЎдЈЁtЈ©ЎЭgЎдЈЁ
Ј¬gЎдЈЁtЈ©ЎЭgЎдЈЁ ![]() Ј©=6Ј¬
Ј©=6Ј¬
јґєЇКэgЈЁtЈ©ФЪt ![]() КЗФцєЇКэЈ¬ЛщТФµ±t=
КЗФцєЇКэЈ¬ЛщТФµ±t= ![]() К±Ј¬gЈЁtЈ©ИЎЧоРЎЦµ
К±Ј¬gЈЁtЈ©ИЎЧоРЎЦµ ![]() Ј¬
Ј¬
ТтґЛµ±k= ![]() К±Ј¬|AB|2+|DE|2µДЧоРЎЦµОЄ
К±Ј¬|AB|2+|DE|2µДЧоРЎЦµОЄ ![]() Ј®
Ј®
ЎѕЅвОцЎїЈЁ1Ј©НЁ№эFЈЁ0Ј¬ ![]() Ј©Ј¬ФІРДQФЪПЯ¶ОOFЖЅ·ЦПЯy=
Ј©Ј¬ФІРДQФЪПЯ¶ОOFЖЅ·ЦПЯy= ![]() ЙПЈ¬НЖіцЗуіцp=1Ј¬НЖіцЕЧОпПЯCµД·ЅіМЈ®ЈЁ2Ј©јЩЙиґжФЪµгMЈЁx0 Ј¬
ЙПЈ¬НЖіцЗуіцp=1Ј¬НЖіцЕЧОпПЯCµД·ЅіМЈ®ЈЁ2Ј©јЩЙиґжФЪµгMЈЁx0 Ј¬ ![]() Ј©Ј¬ЈЁx0/span>Јѕ0Ј©ВъЧгМхјюЈ¬ЕЧОпПЯCФЪµгMґ¦µДЗРПЯµДР±ВКОЄєЇКэµДµјКэЈ¬ЗуіцQµДЧш±кЈ¬АыУГ|QM|=|OQ|Ј¬ЗуіцMЈЁ
Ј©Ј¬ЈЁx0/span>Јѕ0Ј©ВъЧгМхјюЈ¬ЕЧОпПЯCФЪµгMґ¦µДЗРПЯµДР±ВКОЄєЇКэµДµјКэЈ¬ЗуіцQµДЧш±кЈ¬АыУГ|QM|=|OQ|Ј¬ЗуіцMЈЁ ![]() Ј©Ј®К№µГЦ±ПЯMQУлЕЧОпПЯCПаЗРУлµгMЈ®ЈЁ3Ј©µ±x0=
Ј©Ј®К№µГЦ±ПЯMQУлЕЧОпПЯCПаЗРУлµгMЈ®ЈЁ3Ј©µ±x0= ![]() К±Ј¬ЗуіцЎСQµД·ЅіМОЄЈ®АыУГЦ±ПЯУлЕЧОпПЯ·ЅіМБЄБў·ЅіМЧйЈ®ЙиAЈЁx1 Ј¬ y1Ј©Ј¬BЈЁx2 Ј¬ y2Ј©Ј¬АыУГО¤ґп¶ЁАнЈ¬Зуіц|AB|2 Ј® Н¬АнЗуіц|DE|2 Ј¬ НЁ№э|AB|2+|DE|2µД±нґпКЅЈ¬НЁ№э»»ФЄЈ¬АыУГµјКэЗуіцєЇКэµДЧоРЎЦµЈ®
К±Ј¬ЗуіцЎСQµД·ЅіМОЄЈ®АыУГЦ±ПЯУлЕЧОпПЯ·ЅіМБЄБў·ЅіМЧйЈ®ЙиAЈЁx1 Ј¬ y1Ј©Ј¬BЈЁx2 Ј¬ y2Ј©Ј¬АыУГО¤ґп¶ЁАнЈ¬Зуіц|AB|2 Ј® Н¬АнЗуіц|DE|2 Ј¬ НЁ№э|AB|2+|DE|2µД±нґпКЅЈ¬НЁ№э»»ФЄЈ¬АыУГµјКэЗуіцєЇКэµДЧоРЎЦµЈ®


 СѧѧϰєГ°пКЦПµБРґр°ё
СѧѧϰєГ°пКЦПµБРґр°ё РЎС§Н¬ІЅИэБ·єЛРДГЬѕнПµБРґр°ё
РЎС§Н¬ІЅИэБ·єЛРДГЬѕнПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№ІПнµҐіµЖуТµФЪ![]() іЗКРѕНЎ°Т»МмЦРТ»БѕµҐіµµДЖЅѕщіЙ±ѕУлЧвУГµҐіµКэБїЦ®јдµД№ШПµЎ±ЅшРРБЛµчІйЈ¬ІўЅ«Па№ШКэѕЭНіјЖИзПВ±нЈє
іЗКРѕНЎ°Т»МмЦРТ»БѕµҐіµµДЖЅѕщіЙ±ѕУлЧвУГµҐіµКэБїЦ®јдµД№ШПµЎ±ЅшРРБЛµчІйЈ¬ІўЅ«Па№ШКэѕЭНіјЖИзПВ±нЈє

ёщѕЭТФЙПКэѕЭЈ¬СРѕїИЛФ±ЙијЖБЛБЅЦЦІ»Н¬µД»Ш№й·ЦОцДЈРНЈ¬µГµЅБЅёцДвєПєЇКэЈє
ДЈРНјЧЈє![]() Ј¬ДЈРНТТЈє
Ј¬ДЈРНТТЈє![]() .
.
ЈЁ1Ј©ОЄБЛЖАјЫБЅЦЦДЈРНµДДвєПР§№ыЈ¬НкіЙТФПВИООсЈє
ўЩНкіЙПВ±нЈЁјЖЛгЅб№ыѕ«И·µЅ0.1ФЄЈ©ЈЁ±ёЧўЈє![]() Ј¬
Ј¬![]() іЖОЄПаУ¦УЪµг
іЖОЄПаУ¦УЪµг![]() µДІРІоЈ©Ј»
µДІРІоЈ©Ј»

ўЪ·Ц±рјЖЛгДЈРНјЧУлДЈРНТТµДІРІоЖЅ·ЅєН![]() ј°
ј°![]() Ј¬ІўНЁ№э±ИЅП
Ј¬ІўНЁ№э±ИЅП![]() µДґуРЎЈ¬ЕР¶ПДДёцДЈРНДвєПР§№ыёьєГ.
µДґуРЎЈ¬ЕР¶ПДДёцДЈРНДвєПР§№ыёьєГ.
ЈЁ2Ј©ХвјТЖуТµФЪ4іЗКРН¶·Е№ІПнµҐіµєуЈ¬КЬµЅ№гґуКРГсµДИИБТ»¶УІў№©І»У¦ЗуЈ¬УЪКЗёГЖуТµѕц¶ЁФцјУµҐіµН¶·ЕБї.ёщѕЭКРіЎµчІйЈ¬КРіЎН¶·ЕБїґпµЅ1НтБѕК±Ј¬ЖЅѕщГїБѕµҐіµТ»МмДЬКХИл7.2ФЄЈ»КРіЎН¶·ЕБїґпµЅ1.2НтБѕК±Ј¬ЖЅѕщГїБѕµҐіµТ»МмДЬКХИл6.8ФЄ.Иф°ґЈЁ1Ј©ЦРДвєПР§№ыЅПєГµДДЈРНјЖЛгТ»МмЦРТ»БѕµҐіµµДЖЅѕщіЙ±ѕЈ¬ОКёГЖуТµН¶·ЕБїСЎФс1НтБѕ»№КЗ1.2НтБѕДЬ»сµГёь¶аАыИуЈїЗлЛµГчАнУЙ.ЈЁАыИу![]() КХИл
КХИл![]() іЙ±ѕЈ©
іЙ±ѕЈ©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіЖуТµОЄБЛЅвПВКфДіІїГЕ¶Ф±ѕЖуТµЦ°№¤µД·юОсЗйїцЈ¬Лж»ъ·ГОК50ГыЦ°№¤Ј¬ёщѕЭХв50ГыЦ°№¤¶ФёГІїГЕµДЖА·ЦЈ¬»жЦЖЖµВК·ЦІјЦ±·ЅНјЈЁИзНјЛщКѕЈ©Ј¬ЖдЦРСщ±ѕКэѕЭ·ЦЧйЗшјдОЄ![]()

ЈЁ1Ј©ЗуЖµВК·ЦІјЦ±·ЅНјЦР![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©№АјЖёГЖуТµµДЦ°№¤¶ФёГІїГЕЖА·ЦІ»µНУЪ80µДёЕВКЈ»
ЈЁ3Ј©ґУЖА·ЦФЪ![]() µДКЬ·ГЦ°№¤ЦРЈ¬Лж»ъійИЎ2ИЛЈ¬ЗуґЛ2ИЛЖА·Ц¶јФЪ
µДКЬ·ГЦ°№¤ЦРЈ¬Лж»ъійИЎ2ИЛЈ¬ЗуґЛ2ИЛЖА·Ц¶јФЪ![]() µДёЕВК.
µДёЕВК.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪТ»ґОКэС§ІвСйєуЈ¬°ај¶С§ОЇ¶ФСЎґрМвµДСЎМвЗйїцЅшРРНіјЖЈ¬ИзПВ±нЈє
јёєОЦ¤ ГчСЎЅІ | ј«Чш±кУл ІОКэ·ЅіМ | І»µИКЅ СЎЅІ | єПјЖ | |
ДРН¬С§ | 12 | 4 | 6 | 22 |
Е®Н¬С§ | 0 | 8 | 12 | 20 |
єПјЖ | 12 | 12 | 18 | 42 |
ЈЁ1Ј©ФЪНіјЖЅб№ыЦРЈ¬Из№ы°СјёєОЦ¤ГчСЎЅІєНј«Чш±кУлІОКэ·ЅіМіЖОЄЎ°јёєОАаЎ±Ј¬°СІ»µИКЅСЎЅІіЖОЄЎ°ґъКэАаЎ±Ј¬ОТГЗїЙТФµГµЅИзПВ2ЎБ2БРБЄ±н.
јёєОАа | ґъКэАа | єПјЖ | |
ДРН¬С§ | 16 | 6 | 22 |
Е®Н¬С§ | 8 | 12 | 20 |
єПјЖ | 24 | 18 | 42 |
ДЬ·сИПОЄСЎЧцЎ°јёєОАаЎ±»тЎ°ґъКэАаЎ±УлРФ±рУР№ШЈ¬ИфУР№ШЈ¬ДгУР¶аґуµД°СОХЈї
ЈЁ2Ј©ФЪФКјНіјЖЅб№ыЦРЈ¬Из№ыІ»їјВЗРФ±рТтЛШЈ¬°ґ·ЦІгійСщµД·Ѕ·ЁґУСЎЧцІ»Н¬СЎґрМвµДН¬С§ЦРЛж»ъСЎіц7ГыН¬С§ЅшРРЧщМёЈ®ТСЦЄХвГыС§ОЇєН2ГыКэС§їОґъ±н¶јФЪСЎЧцЎ°І»µИКЅСЎЅІЎ±µДН¬С§ЦРЈ®
ўЩЗуФЪХвГыС§ОЇ±»СЎЦРµДМхјюПВЈ¬2ГыКэС§їОґъ±нТІ±»СЎЦРµДёЕВКЈ»
ўЪјЗійИЎµЅКэС§їОґъ±нµДИЛКэОЄ![]() Ј¬Зу
Ј¬Зу![]() µД·ЦІјБРј°КэС§ЖЪНы
µД·ЦІјБРј°КэС§ЖЪНы![]() Ј®
Ј®
ПВГжБЩЅзЦµ±нЅц№©ІОїјЈє
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙиНЦФІ ![]() µДЧуУТ¶Ґµг·Ц±рОЄAЈ¬BЈ¬µгPФЪНЦФІЙПЗТТмУЪAЈ¬BБЅµгЈ¬OОЄЧш±кФµгЈ®
µДЧуУТ¶Ґµг·Ц±рОЄAЈ¬BЈ¬µгPФЪНЦФІЙПЗТТмУЪAЈ¬BБЅµгЈ¬OОЄЧш±кФµгЈ®
ЈЁ1Ј©ИфЦ±ПЯAPУлBPµДР±ВКЦ®»эОЄ ![]() Ј¬ЗуНЦФІµДАлРДВКЈ»
Ј¬ЗуНЦФІµДАлРДВКЈ»
ЈЁ2Ј©Иф|AP|=|OA|Ј¬Ц¤ГчЦ±ПЯOPµДР±ВКkВъЧг|k|Јѕ ![]() Ј®
Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїС§РЈТХКхЅЪ¶ФН¬Т»АаµД![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ЛДПоІОИьЧчЖ·Ј¬Ц»ЖАТ»ПоТ»µИЅ±Ј¬ФЪЖАЅ±ЅТПюЗ°Ј¬јЧЎўТТЎў±ыЎў¶ЎЛДО»Н¬С§¶ФХвЛДПоІОИьЧчЖ·Ф¤ІвИзПВЈє
ЛДПоІОИьЧчЖ·Ј¬Ц»ЖАТ»ПоТ»µИЅ±Ј¬ФЪЖАЅ±ЅТПюЗ°Ј¬јЧЎўТТЎў±ыЎў¶ЎЛДО»Н¬С§¶ФХвЛДПоІОИьЧчЖ·Ф¤ІвИзПВЈє
јЧЛµЈєЎ°КЗ![]() »т
»т![]() ЧчЖ·»сµГТ»µИЅ±Ў±Ј»
ЧчЖ·»сµГТ»µИЅ±Ў±Ј»
ТТЛµЈєЎ°![]() ЧчЖ·»сµГТ»µИЅ±Ў±Ј»
ЧчЖ·»сµГТ»µИЅ±Ў±Ј»
±ыЛµЈєЎ°![]() Ј¬
Ј¬![]() БЅПоЧчЖ·Оґ»сµГТ»µИЅ±Ў±Ј»
БЅПоЧчЖ·Оґ»сµГТ»µИЅ±Ў±Ј»
¶ЎЛµЈєЎ°КЗ![]() ЧчЖ·»сµГТ»µИЅ±Ў±.
ЧчЖ·»сµГТ»µИЅ±Ў±.
ИфХвЛДО»Н¬С§ЦРЦ»УРБЅО»ЛµµД»°КЗ¶ФµДЈ¬Фт»сµГТ»µИЅ±µДЧчЖ·КЗ__________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДі№«ЛѕЙъІъјЧЎўТТБЅЦЦІъЖ·ЛщµГАыИу·Ц±рОЄ![]() єН
єН![]() ЈЁНтФЄЈ©Ј¬ЛьГЗУлН¶ИлЧКЅрЈЁНтФЄЈ©µД№ШПµУРѕС鹫ʽ
ЈЁНтФЄЈ©Ј¬ЛьГЗУлН¶ИлЧКЅрЈЁНтФЄЈ©µД№ШПµУРѕС鹫ʽ![]() Ј¬
Ј¬![]() Ј®ЅсЅ«120НтФЄЧКЅрН¶ИлЙъІъјЧЎўТТБЅЦЦІъЖ·Ј¬ІўТЄЗу¶ФјЧЎўТТБЅЦЦІъЖ·µДН¶ЧКЅр¶о¶јІ»µНУЪ20НтФЄЈ®
Ј®ЅсЅ«120НтФЄЧКЅрН¶ИлЙъІъјЧЎўТТБЅЦЦІъЖ·Ј¬ІўТЄЗу¶ФјЧЎўТТБЅЦЦІъЖ·µДН¶ЧКЅр¶о¶јІ»µНУЪ20НтФЄЈ®
ЈЁўсЈ©Йи¶ФТТІъЖ·Н¶ИлЧКЅр![]() НтФЄЈ¬ЗуЧЬАыИу
НтФЄЈ¬ЗуЧЬАыИу![]() ЈЁНтФЄЈ©№ШУЪ
ЈЁНтФЄЈ©№ШУЪ![]() µДєЇКэ№ШПµКЅј°Жд¶ЁТеУтЈ»
µДєЇКэ№ШПµКЅј°Жд¶ЁТеУтЈ»
ЈЁўтЈ©ИзєО·ЦЕдК№УГЧКЅрЈ¬ІЕДЬК№ЛщµГЧЬАыИуЧоґуЈїЧоґуАыИуОЄ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
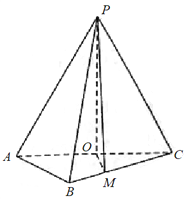
ЎѕМвДїЎїИзНјЈ¬ФЪИэАвЧ¶![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОЄ
ОЄ![]() µДЦРµгЈ®
µДЦРµгЈ®
ЈЁ1Ј©Ц¤ГчЈє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©Ифµг![]() ФЪАв
ФЪАв![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ![]() Ј¬Зуµг
Ј¬Зуµг![]() µЅЖЅГж
µЅЖЅГж![]() µДѕаАлЈ®
µДѕаАлЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіРЛИ¤РЎЧйУыСРѕїЦзТ№ОВІоґуРЎУл»јёРГ°ИЛКэ¶аЙЩЦ®јдµД№ШПµЈ¬ЛыГЗ·Ц±рµЅЖшПуѕЦУлДіТЅФєіВјБЛ1ЦБ6ФВ·ЭГїФВ10єЕµДЦзТ№ОВІоЗйїцУлТт»јёРГ°¶шѕНХпµДИЛКэЈ¬µГµЅИзПВЧКБПЈє
ИХЖЪ | 1ФВ10ИХ | 2ФВ10ИХ | 3ФВ10ИХ | 4ФВ10ИХ | 5ФВ10ИХ | 6ФВ10ИХ |
ЦзТ№ОВІо | 10 | 11 | 13 | 12 | 8 | 6 |
ѕНХпИЛКэ | 22 | 25 | 29 | 26 | 16 | 12 |
ёГРЛИ¤РЎЧйИ·¶ЁµДСРѕї·Ѕ°ёКЗЈєПИґУХвБщЧйКэѕЭЦРСЎИЎ2ЧйЈ¬УГКЈПВµД4ЧйКэѕЭЗуПЯРФ»Ш№й·ЅіМЈ¬ФЩУГ±»СЎИЎµД2ЧйКэѕЭЅшРРјмСйЈ®
ЈЁўсЈ©ИфСЎИЎµДКЗ1ФВУл6ФВµДБЅЧйКэѕЭЈ¬ЗлёщѕЭ2ФВЦБ5ФВ·ЭµДКэѕЭЈ¬Зуіцy№ШУЪxµДПЯРФ»Ш№й·ЅіМ![]() ЈЅ
ЈЅ![]() xЈ«
xЈ«![]() Ј»
Ј»
ЈЁўтЈ©ИфУЙПЯРФ»Ш№й·ЅіМµГµЅµД№АјЖКэѕЭУлЛщСЎіцµДјмСйКэѕЭµДОуІоѕщІ»і¬№э2ИЛЈ¬ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗАнПлµДЈ¬КФОКёГРЎЧйЛщµГПЯРФ»Ш№й·ЅіМКЗ·сАнПлЈ®
ёЅЈє ЈЁІОїјКэѕЭ
ЈЁІОїјКэѕЭ![]() Ј©
Ј©
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com