
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)因为l1⊥l2,得a(a-1)+b=0.①又l1过点(1,1),所以a+b=0.②联立①②可得结果,要进行检验,当a=0,b=0,方程![]() 不成立舍去(2)因为l1∥l2,所以a-b(a-1)=0,③由题意知a>0,b>0,直线l2与两坐标轴的交点坐标分别为
不成立舍去(2)因为l1∥l2,所以a-b(a-1)=0,③由题意知a>0,b>0,直线l2与两坐标轴的交点坐标分别为![]() 则
则![]() ,
,
联立求![]() .
.
试题解析:
(1)∵l1⊥l2,∴a(a-1)+b=0.①
又l1过点(1,1),∴a+b=0.②
由①②,解得![]() 或
或![]() .
.
当a=0,b=0时不合题意,舍去.
∴a=2,b=-2.
(2)∵l1∥l2,∴a-b(a-1)=0,③
由题意知a>0,b>0,直线l2与两坐标轴的交点坐标分别为![]()
则![]() ,
,
得ab=4,④
由③④,得a=2,b=2.


科目:高中数学 来源: 题型:
【题目】某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( ) 
A.45
B.50
C.55
D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
E是PC的中点.求证:

(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E、F分别是棱DD1、C1D1的中点. (Ⅰ)证明:平面ADC1B1⊥平面A1BE;
(Ⅱ)证明:B1F∥平面A1BE;
(Ⅲ)若正方体棱长为1,求四面体A1﹣B1BE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在区间[t,t+2](t>0)上的最小值;
(2)对一切实数x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),lnx> ![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题: ①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
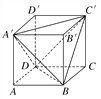
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com