练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．过原点O作圆x2+y2-8x=0的弦OA，延长OA到N，使|OA|=|AN|，求点N的轨迹方程．

    分析 设N（x，y），延长OA到N，使|OA|=|AN|，可得A$（\frac{x}{2}，\frac{y}{2}）$．由于点A在圆（x′）2+（y′）2-8x′=0上，即可得出．

    解答 解：设N（x，y），∵延长OA到N，使|OA|=|AN|，∴A$（\frac{x}{2}，\frac{y}{2}）$．
    由于点A在圆（x′）2+（y′）2-8x′=0上，
    ∴$（\frac{x}{2}）^{2}+（\frac{y}{2}）^{2}$-8×$\frac{x}{2}$=0，化为：x2+y2-16x=0，即为点N的轨迹方程．

    点评 本题考查了圆的方程、中点坐标公式、“代点法”，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．设0＜α＜$\frac{π}{2}$＜β＜π，sinα=$\frac{3}{5}，sin（α+β）=\frac{3}{5}$，则sinβ的值为$\frac{24}{25}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．函数y=sin（2x+$\frac{π}{3}$ ）的一条对称轴为（　　）
    A．x=$\frac{π}{2}$B．x=0C．x=-$\frac{π}{6}$D．x=$\frac{π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设等比数列{an}的前n项和为Sn，满足对任意的正整数n，均有Sn+3=8Sn+3，则a1=$\frac{3}{7}$，公比q=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

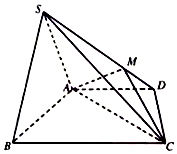    6．如图，在四棱锥S-ABCD中，底面梯形ABCD中，AD∥BC，平面SAB⊥平面ABCD，△SAB是等边三角形，已知$AC=2AB=4，BC=2AD=2CD=2\sqrt{5}$，M是SD上任意一点，$\overrightarrow{SM}=m\overrightarrow{MD}$，且m＞0．
    （1）求证：平面SAB⊥平面MAC；
    （2）试确定m的值，使三棱锥S-ABC体积为三棱锥S-MAC体积的3倍．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设集合A={x|1＜x＜2}，B={x|x＜a}满足A?B，则实数a的取值范围是（　　）
    A．[2，+∞）B．（-∞，1]C．[1，+∞）D．（-∞，2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．以椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的中心为原点，左焦点为焦点的抛物线的标准方程是（　　）
    A．x2=8yB．y2=16xC．x2=-8yD．y2=-16x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点（1，$\frac{\sqrt{3}}{2}$），椭圆的左、右顶点分别为A1，A2，点P坐标为（4，0），|PA1|，|A1A2|，|PA2|成等差数列．
    （1）求椭圆的标准方程；
    （2）椭圆内部是否存在一个定点，过此点的直线交椭圆于M，N两点，且$\overrightarrow{PM}$•$\overrightarrow{PN}$=12恒成立，若存在，求出此点，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知等差数列{an}与等差数列{bn}的前n项和分别为Sn和Tn，若$\frac{S_n}{T_n}=\frac{3n-1}{2n+3}$，则$\frac{{{a_{10}}}}{{{b_{10}}}}$=（　　）
    A．$\frac{3}{2}$B．$\frac{14}{13}$C．$\frac{56}{41}$D．$\frac{29}{23}$

    查看答案和解析>>

    同步练习册答案