
分析 (1)从4个10分题和3个20分题中各抽取1题的基本事件总数n=12,“得30分”这一事件包含的基本事件个数m=3,由此利用等可能事件概率计算公式能求出甲选手恰好得30分的概率.
(Ⅱ)“得分超过10分”这一事件包含的基本事件个数k=4,由此利用等可能事件概率计算公式能求出甲选手得分超过10分的概率.
解答 解:(1)从天而降个10分题和3个20分题中各抽取1题的基本事件空间:
Ω={(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),(A4,B1),(A4,B2),(A4,B3)},
基本事件总数n=12.(4分)
设“得30分”这一事件为M,则M={(A1,B2),(A3,B2),(A4,B2)},M中包含的基本事件个数m=3.
∴甲选手恰好得30分的概率为P(M)=$\frac{m}{n}=\frac{3}{12}$=$\frac{1}{4}$.(8分)
(Ⅱ)设“得分超过10分”这一事件为N,
则N={(A2,B2),(A1,B2),(A3,B2),(A4,B2)},
N中包含的基本事件个数k=4.
∴甲选手得分超过10分的概率为P(N)=$\frac{k}{n}=\frac{4}{12}=\frac{1}{3}$.(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0秒、2秒或6秒 | B. | 2秒或16秒 | C. | 2秒、8秒或16秒 | D. | 2秒或6秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
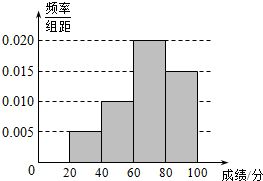 某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )
某班学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是18人,则该班的学生人数是( )| A. | 45 | B. | 50 | C. | 55 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos(x+$\frac{π}{2}$) | B. | y=1-2cos22x | C. | y=-x2 | D. | y=|sin(π-x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒小于0 | B. | 恒大于0 | C. | 可能等于0 | D. | 可正也可负 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com