
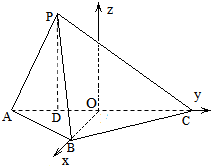
如图所示,在三棱锥PABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.

(1)求证:AB⊥平面PBC;
(2)设AB=BC,直线PA与平面ABC所成的角为45°,求异面直线AP与BC所成的角;
(3)在(2)的条件下,求二面角C-PA-B的余弦值.
(1)由PC⊥平面ABC,得AB⊥PC.由点C在平面PBA内的射影D在直线PB上,
得到CD⊥平面PAB.进一步推出AB⊥平面PBC.
(2)异面直线AP与BC所成的角为60°.

(3)所求二面角的余弦值为 .
.
【解析】
试题分析:(1)∵PC⊥平面ABC,AB?平面ABC,
∴AB⊥PC.∵点C在平面PBA内的射影D在直线PB上,
∴CD⊥平面PAB.
又∵AB?平面PBA,∴AB⊥CD.
又∵CD∩PC=C,∴AB⊥平面PBC.
(2)∵PC⊥平面ABC,
∴∠PAC为直线PA与平面ABC所成的角.
于是∠PAC=45°,设AB=BC=1,则PC=AC= ,以B为原点建立如图所示的空间直角坐标系,则B(0,0,0),A(0,1,0),C(1,0,0),P(1,0,
,以B为原点建立如图所示的空间直角坐标系,则B(0,0,0),A(0,1,0),C(1,0,0),P(1,0, ),
),
 =(1,-1,
=(1,-1, ),
), =(1,0,0),
=(1,0,0),
∵cos〈 ,
, 〉=
〉= =
=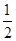 ,∴异面直线AP与BC所成的角为60°.
,∴异面直线AP与BC所成的角为60°.

(3)取AC的中点E,连接BE,则 =(
=(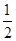 ,
,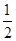 ,0),
,0),
∵AB=BC,∴BE⊥AC.又∵平面PCA⊥平面ABC,
∴BE⊥平面PAC.∴ 是平面PAC的法向量.设平面PAB的法向量为n=(x,y,z),则由
是平面PAC的法向量.设平面PAB的法向量为n=(x,y,z),则由 得
得 取z=1,得
取z=1,得
∴n=(- ,0,1).
,0,1).
于是cos〈n, 〉=
〉= =
= =-
=- .
.
又∵二面角C-PA-B为锐角,∴所求二面角的余弦值为 .
.
考点:本题主要考查立体几何中的垂直关系、角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。注意运用转化与化归思想,将空间问题转化成平面问题。


科目:高中数学 来源: 题型:
 (2012•广州一模)如图所示,在三棱锥P-ABC中,AB=BC=
(2012•广州一模)如图所示,在三棱锥P-ABC中,AB=BC=| 6 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在三棱锥P-ABC中,AB=BC=
如图所示,在三棱锥P-ABC中,AB=BC=| 6 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
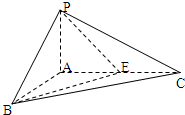 如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB⊥AC,AB=AC=2,E为AC的中点.
如图所示,在三棱锥P-ABC中,PA⊥平面ABC,PA=1,AB⊥AC,AB=AC=2,E为AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com