
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
【答案】4π
【解析】
设出球心的位置,利用勾股定理列方程组,解方程组求得球的半径,进而求得球的表面积.
长方形ABCD中,AB=1,∠ABD=60°,可得BD=2,AD![]() ,
,
作AE⊥BD于E,可得AEBD=ABAD,所以AE![]() ,BE
,BE![]() ,
,
因为平面ABD⊥平面BCD,AE![]() 面ABD,平面ABD∩平面BCD=BD,所以AE⊥面BCD,
面ABD,平面ABD∩平面BCD=BD,所以AE⊥面BCD,
由直角三角形BCD可得其外接圆的圆心为斜边BD的中点O1,且外接圆的半径r![]() 1,过O1作OO1垂直于底面BCD,所以EO1=O1B﹣BE=1
1,过O1作OO1垂直于底面BCD,所以EO1=O1B﹣BE=1![]() ,
,
所以OO1∥AE,取三棱锥外接球的球心O,设外接球的半径为R,
作OF⊥AE于F,则四边形EFOO1为矩形,O1E=OF,EF=OO1,则OA=OC=OB=OD=R,
在△AFO中,OA2=AF2+OF2=(AE﹣EF)2+EO12即R2=(![]() OO1)2
OO1)2![]() ;①
;①
在△BOO1中:OB2=OO12+EO12,即R2=OO12![]() ;②
;②
由①②可得R2=1,OO1=0,即外接球的球心为O1,所以外接球的表面积S=4πR2=4π,
故答案为:4π



 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位考察了甲乙两种不同的农产品加工生产方式,现对两种生产方式加工的产品质量进行测试并打分对比,得到如下数据:
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 60 | 50 | 30 |
其中产品质量按测试指标可划分为:指标在区间![]() 上的为特优品,指标在区间
上的为特优品,指标在区间![]() 上的为一等品,指标在区间
上的为一等品,指标在区间![]() 上的为二等品.
上的为二等品.
(1)用事件![]() 表示“按照生产方式甲生产的产品为特优品”,估计
表示“按照生产方式甲生产的产品为特优品”,估计![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断能否有![]() 的把握认为“特优品”与生产方式有关?
的把握认为“特优品”与生产方式有关?
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
(3)根据打分结果对甲乙两种生产方式进行优劣比较.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: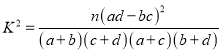 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面凸六边形![]() 的边长相等,其中
的边长相等,其中![]() 为矩形,
为矩形,![]() .将
.将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折至
折至![]() ,
,![]() ,且均在同侧与平面
,且均在同侧与平面![]() 垂直,连接
垂直,连接![]() ,如图所示,E,G分别是
,如图所示,E,G分别是![]() ,
,![]() 的中点.
的中点.
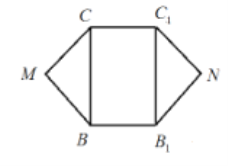
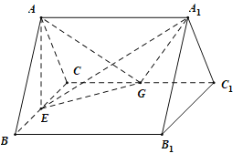
(1)求证:多面体![]() 为直三棱柱;
为直三棱柱;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若正项数列![]() 的首项为
的首项为![]() ,且当数列
,且当数列![]() 是公比为
是公比为![]() 的等比数列时,则称数列
的等比数列时,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:数列
,证明:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若数列![]() 为“
为“![]() 数列”,且对任意
数列”,且对任意![]() ,
,![]() 、
、![]() 、
、![]() 成等差数列,公差为
成等差数列,公差为![]() .
.
①求![]() 与
与![]() 间的关系;
间的关系;
②若数列![]() 为递增数列,求
为递增数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com