分析:(1)要证直线与直线垂直,首先把一个直线放到一个已知平面上,根据直线与平面垂直的判定定理做出线与面垂直,进而证得线与线垂直.
(2)以点D1为坐标原点,D1B1,D1A1,D1P所在直线分别为x轴,y轴,z轴,建立空间坐标系D1-xyz,平面PAA1所在平面为坐标平面yOz,取平面PAA1的一个法向量,根据两个向量之间的夹角得到二面角的大小.
解答:解:(1)证明:设B
1C
1的中点为D
1,∵PB
1=PC
1,∴PD
1⊥B
1C
1,
又∵△A
1B
1C
1是正三角形,∴A
1D
1⊥B
1C
1,∴B
1C
1⊥平面PA
1D
1,
∴PA
1⊥B
1C
1,
又∵BC∥B
1C
1,∴PA
1⊥BC;
(2)∵平面PB
1BCC
1⊥平面A
1B
1C
1,∴PD
1⊥平面A
1B
1C
1,
又∵AA
1⊥平面A
1B
1C
1,∴A,A
1,P,D
1四点共面,
如图,以点D
1为坐标原点,D
1B
1,D
1A
1,D
1P所在直线分别为x轴,y轴,z轴,建立空间坐标系D
1-xyz,
平面PAA
1所在平面为坐标平面yOz,取平面PAA
1的一个法向量
=(1,0,0)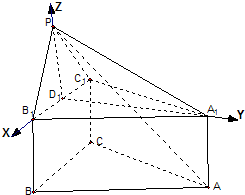
由
PC1=PB1=,B1C1=2得到PD
1=1,
由A
1B
1=B
1C
1=C
1A
1=2得到
A1D1=,
点P的坐标为(0,0,1),点A
1的坐标为
(0,,0),
点C
1的坐标为(-1,0,0),
设平面PC
1A
1的法向量为
=(x,y,z),
则
•=(x,y,z)•(0,,-1)=0,所以
z=y•=(x,y,z)•(-1,0,-1)=0,所以x=-z,
令y=1,则
=(-,1,),
cos?,>==-,
即所求二面角是
arccos.
点评:本题考查利用空间向量解决几何体中的夹角的问题,本题解题的关键是建立合适的坐标系,把逻辑性很强的理论推导转化成数字的运算,降低了题目的难度.

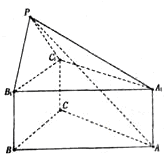 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点P在平面BCC1B1内,PB1=PC1=
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点P在平面BCC1B1内,PB1=PC1= 由PC1=PB1=
由PC1=PB1=

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.