Question

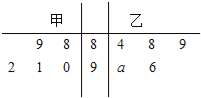
【题目】某机械厂今年进行了五次技能考核，其中甲、乙两名技术骨干得分的平均分相等，成绩统计情况如茎叶图所示（其中是09的某个整数）

（1）若该厂决定从甲乙两人中选派一人去参加技能培训，从成绩稳定性角度考虑，你认为谁去比较合适？

（2）若从甲的成绩中任取两次成绩作进一步分析，在抽取的两次成绩中，求至少有一次成绩在（90，100]之间的概率．

Answer 1

【答案】（1）从成绩稳定性角度考虑，我认为甲去比较合适；（2）.

【解析】试题分析：(1)第一步，根据平均分相等，计算，第二步计算方差和，最后比较大小，方差小说明成绩比较稳定；

（2）甲有5个成绩，其中有2个，有3个，那么首先计算5个成绩选2个成绩的所有方法，然后计算至少有一次成绩在的方法，最后相除就是所求概率.

试题解析：解：（1）由已知中的茎叶图可得：

甲的平均分为：（88+89+90+91+92）=90，

由甲、乙两名技术骨干得分的平均分相等，

故乙的平均分：（84+88+89+90+a+96）=90，解得：a=3，

则=[（88﹣90）2+（89﹣90）2+（90﹣90）2+（91﹣90）2+（92﹣90）2]=2，

=[（84﹣90）2+（88﹣90）2+（89﹣90）2+（93﹣90）2+（96﹣90）2]="17.2"

∵甲、乙两名技术骨干得分的平均分相等，但＞，

∴从成绩稳定性角度考虑，我认为甲去比较合适，

（2）若从甲的成绩中任取两次成绩作进一步分析，共有=10种不同抽取方法，

其中至少有一次成绩在（90，100]之间有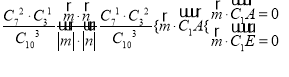 种方法，

故至少有一次成绩在（90，100]之间的概率P=