
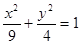 上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____
上的点,F1、F2是两个焦点,则|PF1|·|PF2|的最大值与最小值之差是_____ ≤x≤3+
≤x≤3+ 。根据 函数y=-x2+6x在(3-
。根据 函数y=-x2+6x在(3- ,3)上单调递增,(3,3+
,3)上单调递增,(3,3+ )上单调递减,可求y=-x2+6x的最小值与最大值,从而可求|PF1|?|PF2|的最大值和最小值之差。
)上单调递减,可求y=-x2+6x的最小值与最大值,从而可求|PF1|?|PF2|的最大值和最小值之差。 ,a=3
,a=3 ≤x≤3+
≤x≤3+
 ,3)上单调递增,(3,3+
,3)上单调递增,(3,3+ )上单调递减,
)上单调递减, 时,y=-x2+6x取最小值(3-
时,y=-x2+6x取最小值(3- )(3+
)(3+ )=4,
)=4,

科目:高中数学 来源:不详 题型:单选题
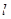 :y=kx+1(k≠0),椭圆E:
:y=kx+1(k≠0),椭圆E: ,若直线
,若直线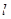 被椭圆E所截弦长为d,则下列直线中被椭圆E所截弦长不是d的直线是( )
被椭圆E所截弦长为d,则下列直线中被椭圆E所截弦长不是d的直线是( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
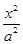 +
+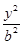 =1(a>b>0)经过点A
=1(a>b>0)经过点A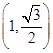 ,且离心率e=
,且离心率e=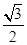 .
. O.若存在,求出直线l的方程;若不存在,说明理由.
O.若存在,求出直线l的方程;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com