
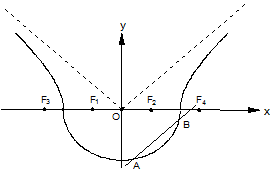
 如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,
如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,分析 (1)由F2(2,0),F3(-6,0),可得$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=36}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,解出即可;
(2)设点A(x1,y1),B(x2,y2),M(x0,y0),设直线l:y=$\frac{b}{a}$(x-m),与椭圆方程联立化为2x2-2mx+(m2-a2)=0,利用△>0,根与系数的关系、中点坐标公式,证明即可.
(3)由(1)知,曲线$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{16}$=1(y≤0)F4(6,0).设直线l1的方程为x=ny+6(n>0).与椭圆方程联立可得(5+4n2)y2+48ny+64=0,利用根与系数的关系、弦长公式、三角形的面积计算公式、基本不等式的性质即可得出.
解答 (1)解:∵F2(2,0),F3(-6,0),
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=36}\\{{a}^{2}-{b}^{2}=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}^{2}=20}\\{{b}^{2}=16}\end{array}\right.$,
则曲线Γ的方程为$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{16}$=1(y≤0)和$\frac{{x}^{2}}{20}-\frac{{y}^{2}}{16}$=1(y>0).
(2)证明:曲线C2的渐近线为y=±$\frac{b}{a}$x,
设直线l:y=$\frac{b}{a}$(x-m),代入C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,化为2x2-2mx+(m2-a2)=0,
△=4m2-8(m2-a2)>0,
解得-$\sqrt{2}$a<m<$\sqrt{2}$a.
又由数形结合知a≤m<$\sqrt{2}$a.
设点A(x1,y1),B(x2,y2),M(x0,y0),
则x1+x2=m,x1x2=$\frac{{m}^{2}-{a}^{2}}{2}$,
∴x0=$\frac{m}{2}$,y0=-$\frac{bm}{2a}$,
∴y0=-$\frac{b}{a}$x0,即点M在直线y=-$\frac{b}{a}$x上.
(3)由(1)知,曲线C1:$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{16}$=1(y≤0),点F4(6,0).
设直线l1的方程为x=ny+6(n>0).
联立化为(5+4n2)y2+48ny+64=0,
△=(48n)2-4×64×(5+4n2)>0,化为n2>1.
设C(x3,y3),D(x4,y4),
∴y3+y4=-$\frac{48n}{5+4{n}^{2}}$,y3y4=$\frac{64}{5+4{n}^{2}}$.
∴|y3-y4|=$\frac{16\sqrt{5}•\sqrt{{n}^{2}-1}}{5+4{n}^{2}}$,
△CDF1面积S=$\frac{1}{2}×8×$$\frac{16\sqrt{5}•\sqrt{{n}^{2}-1}}{5+4{n}^{2}}$,
令t=$\sqrt{{n}^{2}-1}$>0,∴n2=t2+1,
∴S=$\frac{64\sqrt{5}}{4t+\frac{9}{t}}$≤$\frac{16\sqrt{5}}{3}$,当且仅当t=$\frac{3}{2}$,即n=$\frac{\sqrt{13}}{2}$时等号成立,△CDF1面积的最大值为$\frac{16\sqrt{5}}{3}$.
点评 本题考查了椭圆与双曲线的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、三角形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
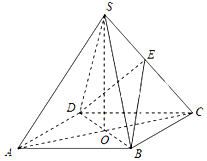 如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “sinα=$\frac{3}{5}$”是“cos2α=$\frac{7}{25}$”的必要不充分条件 | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题是“若xy≠0,则x≠0或y≠0” | |
| C. | 已知命题p:?x∈R,使2x>3x;命题q:?x∈(0,+∞),都有$\frac{1}{{x}^{2}}$<$\frac{1}{{x}^{3}}$,则p∧(¬q)是真命题 | |
| D. | 从匀速传递的生产流水线上,质检员每隔5分钟从中抽取一件产品进行某项指标检测,这是分层抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [-$\frac{\sqrt{3}}{2}$,1] | C. | [0,1+$\frac{\sqrt{3}}{2}$] | D. | [0,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
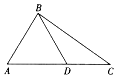 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且sinAsinAcosC+sinCsinAcosA=$\frac{1}{3}$sinC,D为AC边上一点.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且sinAsinAcosC+sinCsinAcosA=$\frac{1}{3}$sinC,D为AC边上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com