
【题目】已知函数f(x)=ln(2ax+1)+ ![]() ﹣x2﹣2ax(a∈R).
﹣x2﹣2ax(a∈R).
(1)若x=2为f(x)的极值点,求实数a的值;
(2)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(3)当a=﹣ ![]() 时,方程f(1﹣x)=
时,方程f(1﹣x)= ![]() 有实根,求实数b的最大值.
有实根,求实数b的最大值.
【答案】
(1)解: ![]() =
= ![]() .…(1分)
.…(1分)
因为x=2为f(x)的极值点,所以f'(2)=0.
即 ![]() ,解得a=0.
,解得a=0.
又当a=0时,f'(x)=x(x﹣2),从而x=2为f(x)的极值点成立
(2)解:因为f(x)在区间[3,+∞)上为增函数,
所以 ![]() 在区间[3,+∞)上恒成立.…(5分)
在区间[3,+∞)上恒成立.…(5分)
①当a=0时,f'(x)=x(x﹣2)≥0在[3,+∞)上恒成立,所以f(x)在[3,+∞)上为增函数,故a=0符合题意.
②当a≠0时,由函数f(x)的定义域可知,必须有2ax+1>0对x≥3恒成立,故只能a>0,
所以2ax2+(1﹣4a)x﹣(4a2+2)≥0对x∈[3,+∞)上恒成立.
令g(x)=2ax2+(1﹣4a)x﹣(4a2+2),其对称轴为 ![]() ,
,
因为a>0所以 ![]() ,从而g(x)≥0在[3,+∞)上恒成立,只要g(3)≥0即可,
,从而g(x)≥0在[3,+∞)上恒成立,只要g(3)≥0即可,
因为g(3)=﹣4a2+6a+1≥0,
解得 ![]() .
.
因为a>0,所以 ![]() .
.
由①可得,a=0时,符合题意;
综上所述,a的取值范围为[0, ![]() ]
]
(3)解:若 ![]() 时,方程
时,方程 ![]() x>0
x>0 ![]() 可化为,
可化为, ![]() .
.
问题转化为b=xlnx﹣x(1﹣x)2+x(1﹣x)=xlnx+x2﹣x3在(0,+∞)上有解,
即求函数g(x)=xlnx+x2﹣x3的值域.
以下给出两种求函数g(x)值域的方法:
方法1:因为g(x)=x(lnx+x﹣x2),令h(x)=lnx+x﹣x2(x>0),
则 ![]() ,
,
所以当0<x<1,h′(x)>0,从而h(x)在(0,1)上为增函数,
当x>1,h′(x)<0,从而h(x')在(1,+∞上为减函数,
因此h(x)≤h(1)=0.
而x>1,故b=xh(x)≤0,
因此当x=1时,b取得最大值0.
方法2:因为g(x)=x(lnx+x﹣x2),所以g'(x)=lnx+1+2x﹣3x2.
设p(x)=lnx+1+2x﹣3x2,则 ![]() .
.
当 ![]() 时,p'(x)>0,所以p(x)在
时,p'(x)>0,所以p(x)在 ![]() 上单调递增;
上单调递增;
当 ![]() 时,p'(x)<0,所以p(x)在
时,p'(x)<0,所以p(x)在 ![]() 上单调递减;
上单调递减;
因为p(1)=0,故必有 ![]() ,又
,又 ![]() ,
,
因此必存在实 ![]() 使得g'(x0)=0,
使得g'(x0)=0,
∴当0<x<x0时,g′(x)<0,所以g(x)在(0,x0)上单调递减;
当x0<x<1,g′(x)>0,所以,g(x)在(x0,1)上单调递增;
又因为 ![]() ,
,
当x→0时,lnx+ ![]() <0,则g(x)<0,又g(1)=0.
<0,则g(x)<0,又g(1)=0.
因此当x=1时,b取得最大值0
【解析】(1)先对函数求导,由x=2为f(x)的极值点,可得f'(2)=0,代入可求a;(2)由题意可得 ![]() 在区间[3,+∞)上恒成立,①当a=0时,容易检验是否符合题意,②当a≠0时,由题意可得必须有2ax+1>0对x≥3恒成立,则a>0,从而2ax2+(1﹣4a)x﹣(4a2+2)≥0对x∈[3,+∞0上恒成立.考查函数g(x)=2ax2+(1﹣4a)x﹣(4a2+2),结合二次函数的性质可求;(3)由题意可得
在区间[3,+∞)上恒成立,①当a=0时,容易检验是否符合题意,②当a≠0时,由题意可得必须有2ax+1>0对x≥3恒成立,则a>0,从而2ax2+(1﹣4a)x﹣(4a2+2)≥0对x∈[3,+∞0上恒成立.考查函数g(x)=2ax2+(1﹣4a)x﹣(4a2+2),结合二次函数的性质可求;(3)由题意可得 ![]() .问题转化为b=xlnx﹣x(1﹣x)2+x(1﹣x)=xlnx+x2﹣x3在(0,+∞)上有解,即求函数g(x)=xlnx+x2﹣x3的值域.方法1:构造函数g(x)=x(lnx+x﹣x2),令h(x)=lnx+x﹣x2(x>0),对函数h(x)求导,利用导数判断函数h(x)的单调性,进而可求
.问题转化为b=xlnx﹣x(1﹣x)2+x(1﹣x)=xlnx+x2﹣x3在(0,+∞)上有解,即求函数g(x)=xlnx+x2﹣x3的值域.方法1:构造函数g(x)=x(lnx+x﹣x2),令h(x)=lnx+x﹣x2(x>0),对函数h(x)求导,利用导数判断函数h(x)的单调性,进而可求
方法2:对函数g(x)=x(lnx+x﹣x2)求导可得g'(x)=lnx+1+2x﹣3x2 . 由导数知识研究函数p(x)=lnx+1+2x﹣3x2 , 的单调性可求函数g(x)的零点,即g'(x0)=0,从而可得函数g(x)的单调性,结合 ![]() ,可知x→0时,lnx+
,可知x→0时,lnx+ ![]() <0,则g(x)<0,又g(1)=0可求b的最大值
<0,则g(x)<0,又g(1)=0可求b的最大值


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、 水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行![]() 天、次年限行
天、次年限行![]() 天共
天共![]() 天)的调查结果:
天)的调查结果:
表二
不限行 | 限行 | 总计 | |
没有雾霾 |
| ||
有雾霾 |
| ||
总计 |
|
|
|
(1)请由表一数据求![]() ,并求在该年11月份任取一天,估计该市是晴天的概率;
,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有![]() 的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
|
|
|
|
|
|
|
|
|
|
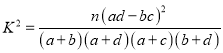
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时,求该函数的值域;
(2)若f(x)>mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、质地相同的红球、黑球各一个,现有放回地随机摸取3次,每次摸取一个球,若摸出红球,得10分,摸出黑球,得5分,则3次摸球所得总分至少是25分的概率是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)(万元),其中固定成本为3万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com