
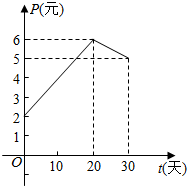
 某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).
某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上(如图).该股票在30天内(包括第30天)的日交易量Q(万股)与时间t(天)的函数关系式为Q=40-t(0≤t≤30且t∈N).分析 (1)根据图象可知此函数为分段函数,在(0,20]和(20,30]两个区间利用待定系数法分别求出一次函数关系式联立可得P的解析式;
(2)因为Q与t成一次函数关系,根据表格中的数据,取出两组即可确定出Q的解析式;根据股票日交易额=交易量×每股较易价格可知y=PQ,可得y的解析式,分别在各段上利用二次函数求最值的方法求出即可.
解答 解:(1)设表示前20天每股的交易价格P(元)与时间t(天)的一次函数关系式为P=k1t+m,
由图象得:$\left\{\begin{array}{l}{2{=k}_{1}×0+m}\\{6{=k}_{1}×20+m}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{5}}\\{m=2}\end{array}\right.$,即P=$\frac{1}{5}$t+2; …(3分)
设表示第20天至第30天每股的交易价格P(元)与时间t(天)的一次函数关系式为P=k2t+n,
即P=-$\frac{1}{10}$t+8.…(6分)
综上知P=$\left\{\begin{array}{l}{\frac{1}{5}t+2,0≤t<20}\\{-\frac{1}{10}t+8,20≤t≤30}\end{array}\right.$(t∈N).…(7分)
(2)由(1)可得y=$\left\{\begin{array}{l}{(\frac{1}{5}t+2)××(40-t),0≤t<20}\\{(-\frac{1}{10}t+8)×(40-t),20≤t≤30}\end{array}\right.,(t∈N)$.
即y=$\left\{\begin{array}{l}{-{\frac{1}{5}t}^{2}+6t+80,0≤t<20}\\{{\frac{1}{10}t}^{2}-12t+320,20≤t≤30}\end{array}\right.(t∈N)$(t∈N).…(10分)
当0≤t<20时,函数y=-$\frac{1}{5}$t2+6t+80的图象的对称轴为直线t=15,
∴当t=15时,ymax=125;
当20≤t≤30时,函数y=$\frac{1}{10}$t2-12t+320的图象的对称轴为直线t=60,
∴该函数在[20,30]上单调递减,即当t=20时,ymax=120.
而125>120,
∴第15天日交易额最大,最大值为125万元. …(13分)
点评 考查学生根据实际问题选择函数类型的能力,理解分段函数的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{1}{13}$] | B. | (0,$\frac{5}{13}$] | C. | [$\frac{1}{13}$,1] | D. | [$\frac{3}{4}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com