
 ,S6=
,S6=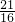 ,bn=λan-n2.
,bn=λan-n2. ,S6=
,S6=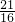 ,
, =
= ,
, =
=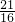 ,
, ,
, ,a1=2.
,a1=2. .
. -n2,
-n2, -(n+1)2<=2λ
-(n+1)2<=2λ -n2,
-n2, <2n+1对任意n∈N*恒成立,
<2n+1对任意n∈N*恒成立, ,当n=1时,-
,当n=1时,- 取得最大值-1,故λ>-1;
取得最大值-1,故λ>-1; ,当n=2时,
,当n=2时, 取得最小值
取得最小值 ,故λ<
,故λ< .
. ,即实数λ的取值范围是(-1,
,即实数λ的取值范围是(-1, ).
). -n2,数列{bn}单调递减,bn+1<bn,可得6λ
-n2,数列{bn}单调递减,bn+1<bn,可得6λ <2n+1对任意n∈N*恒成立,对n分奇数与偶数讨论即可求得实数λ的取值范围.
<2n+1对任意n∈N*恒成立,对n分奇数与偶数讨论即可求得实数λ的取值范围. <2n+1对任意n∈N*恒成立”是关键,也是难点,考查综合分析与运算的能力,属于难题.
<2n+1对任意n∈N*恒成立”是关键,也是难点,考查综合分析与运算的能力,属于难题. 

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com