
分析 (Ⅰ)法一:设A(m,0),B(0,n),M(x,y),利用|AB|2=m2+n2,以及点M为线段AB的中点求解点M的轨迹曲线C的方程.
法二:设O为坐标原点,则$|{OM}|=\frac{1}{2}|{AB}|=1$,判断点M的轨迹曲线C是以原点O为圆心,半径等于1的圆,写出方程即可.
(Ⅱ)法一;通过x2+y2=1,令$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.(θ∈[0,2π))$,转化三角函数求解最值即可.
法二:设t=3x-4y,利用直线3x-4y-t=0与圆C:x2+y2=1有公共点,列出不等式求解即可.
(Ⅲ)假设存在满足题意的t和λ,则设S(x,y),由|ST|=λ|SQ|得:${x^2}+{(y-t)^2}={λ^2}[{x^2}+{(y-\frac{2}{3})^2}]$,化简代入x2+y2=1,推出$(2t-\frac{4}{3}{λ^2})y+\frac{13}{9}{λ^2}-{t^2}-1=0$,推出$t=λ=\frac{3}{2}$,得到结果.
解答 解:(Ⅰ)法一:设A(m,0),B(0,n),M(x,y),则|AB|2=m2+n2①
∵点M为线段AB的中点∴m=2x,n=2y;代入①式得4x2+4y2=4,
即点M的轨迹曲线C的方程为x2+y2=1. …(3分)
法二:设O为坐标原点,则$|{OM}|=\frac{1}{2}|{AB}|=1$,故点M的轨迹曲线C是以原点O为圆心,
半径等于1的圆,其方程为x2+y2=1. …(3分)
(Ⅱ)法一;∵x2+y2=1,∴可令$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.(θ∈[0,2π))$,∴3x-4y=3cosθ-4sinθ=5sin(θ+φ)∈[-5,5].…(7分)
法二:设t=3x-4y,则由题直线3x-4y-t=0与圆C:x2+y2=1有公共点,
∴$\frac{|t|}{{\sqrt{{3^2}+{{(-4)}^2}}}}≤1$,解得t∈[-5,5]…(7分)
(Ⅲ)假设存在满足题意的t和λ,则设S(x,y),由|ST|=λ|SQ|得:${x^2}+{(y-t)^2}={λ^2}[{x^2}+{(y-\frac{2}{3})^2}]$,展开整理得:$({λ^2}-1)({x^2}+{y^2})+(2t-\frac{4}{3}{λ^2})y+\frac{4}{9}{λ^2}-{t^2}=0$,又x2+y2=1,故有$(2t-\frac{4}{3}{λ^2})y+\frac{13}{9}{λ^2}-{t^2}-1=0$,…(9分)
由题意此式对满足x2+y2=1的任意的y都成立,
∴$2t-\frac{4}{3}{λ^2}=0$且$\frac{13}{9}{λ^2}-{t^2}-1=0$,解得:$t=λ=\frac{3}{2}$(∵$t≠\frac{2}{3}$)
所以存在$t=λ=\frac{3}{2}$满足题意要求.…(12分)
点评 本题考查轨迹方程的求法,曲线的参数方程的应用,存在性问题的处理方法,考查转化思想以及计算能力.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
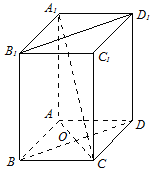 已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.
已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+y2=2016 | B. | x2+(y-2)2=2016 | C. | (x+1)2+(y+1)2=2016 | D. | (x-1)2+(y-1)2=2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{5}}{2}$ | B. | ±$\frac{3}{2}$ | C. | ±$\frac{\sqrt{30}}{5}$ | D. | ±$\frac{3\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com