
°æƒø°øƒ≥“˚¡œ≥ß…˙≤˙![]() ¡Ω÷÷“˚¡œ£Æ…˙≤˙1Õ∞
¡Ω÷÷“˚¡œ£Æ…˙≤˙1Õ∞![]() “˚¡œ£¨–Ë∏√Ãÿ≤˙‘≠¡œ100π´ΩÔ£¨–Ë ±º‰3–° ±£ª…˙≤˙1Õ∞
“˚¡œ£¨–Ë∏√Ãÿ≤˙‘≠¡œ100π´ΩÔ£¨–Ë ±º‰3–° ±£ª…˙≤˙1Õ∞![]() “˚¡œ–Ë∏√Ãÿ≤˙‘≠¡œ100π´ΩÔ£¨–Ë ±º‰1–° ±£¨√øÃÏ
“˚¡œ–Ë∏√Ãÿ≤˙‘≠¡œ100π´ΩÔ£¨–Ë ±º‰1–° ±£¨√øÃÏ![]() “˚¡œµƒ≤˙¡ø≤ª≥¨π˝
“˚¡œµƒ≤˙¡ø≤ª≥¨π˝![]() “˚¡œ≤˙¡øµƒ2±∂£¨√øÃÏ…˙≤˙¡Ω÷÷“˚¡œÀ˘–Ë∏√Ãÿ≤˙‘≠¡œµƒ◊‹¡ø÷¡∂‡750π´ΩÔ£¨√øÃÏ…˙≤˙
“˚¡œ≤˙¡øµƒ2±∂£¨√øÃÏ…˙≤˙¡Ω÷÷“˚¡œÀ˘–Ë∏√Ãÿ≤˙‘≠¡œµƒ◊‹¡ø÷¡∂‡750π´ΩÔ£¨√øÃÏ…˙≤˙![]() “˚¡œµƒ ±º‰≤ªµÕ”⁄…˙≤˙
“˚¡œµƒ ±º‰≤ªµÕ”⁄…˙≤˙![]() “˚¡œµƒ ±º‰£¨√øÕ∞
“˚¡œµƒ ±º‰£¨√øÕ∞![]() “˚¡œµƒ¿˚»Û «√øÕ∞
“˚¡œµƒ¿˚»Û «√øÕ∞![]() “˚¡œ¿˚»Ûµƒ1.5±∂£¨»Ù∏√“˚¡œ≥ß√øÃÏ…˙≤˙
“˚¡œ¿˚»Ûµƒ1.5±∂£¨»Ù∏√“˚¡œ≥ß√øÃÏ…˙≤˙![]() “˚¡œ
“˚¡œ![]() Õ∞£¨
Õ∞£¨![]() “˚¡œ
“˚¡œ![]() Õ∞ ±£®
Õ∞ ±£®![]() £©¿˚»Û◊Ó¥Û£¨‘Ú
£©¿˚»Û◊Ó¥Û£¨‘Ú![]() _____£Æ
_____£Æ
°æ¥∞∏°ø7
°æΩ‚Œˆ°ø
…Ë√øÃÏ![]() ¡Ω÷÷“˚¡œµƒ…˙≤˙ ˝¡ø∑÷± «
¡Ω÷÷“˚¡œµƒ…˙≤˙ ˝¡ø∑÷± «![]() Õ∞£¨
Õ∞£¨![]() Õ∞£¨”…“‚ø…µ√‘º ¯Ãıº˛Œ™£¨
Õ∞£¨”…“‚ø…µ√‘º ¯Ãıº˛Œ™£¨
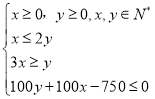 £¨◊˜≥ˆø…––”Ú£¨ƒø±Í∫Ø ˝Œ™
£¨◊˜≥ˆø…––”Ú£¨ƒø±Í∫Ø ˝Œ™![]() £¨∆Ω“∆÷±œfl
£¨∆Ω“∆÷±œfl![]() £¨ø…µ√µ±
£¨ø…µ√µ±![]() π˝
π˝![]() ±£¨
±£¨![]() »°◊Ó¥Û£¨”…¥Àø…µ√
»°◊Ó¥Û£¨”…¥Àø…µ√![]() µƒ÷µ£¨Ω¯∂¯ø…«Û≥ˆ
µƒ÷µ£¨Ω¯∂¯ø…«Û≥ˆ![]() .
.
…Ë√øÃÏ![]() ¡Ω÷÷“˚¡œµƒ…˙≤˙ ˝¡ø∑÷± «
¡Ω÷÷“˚¡œµƒ…˙≤˙ ˝¡ø∑÷± «![]() Õ∞£¨
Õ∞£¨![]() Õ∞£¨‘Ú”–
Õ∞£¨‘Ú”– £¨
£¨
»Ù∫ˆ¬‘![]() £¨‘Ú∆‰±Ì 浃ø…––”Ú»ÁÕº÷–“ı”∞≤ø∑÷À˘ 棨…Ë¿˚»ÛŒ™
£¨‘Ú∆‰±Ì 浃ø…––”Ú»ÁÕº÷–“ı”∞≤ø∑÷À˘ 棨…Ë¿˚»ÛŒ™![]() £¨
£¨
‘Ú![]() £¨¥”∂¯
£¨¥”∂¯![]() £¨
£¨![]() ±Ì æ÷±œfl‘⁄
±Ì æ÷±œfl‘⁄![]() ÷·…œµƒΩÿ懣¨ª≠≥ˆ
÷·…œµƒΩÿ懣¨ª≠≥ˆ![]() £¨
£¨
”…![]() £¨
£¨![]() ø…µ√
ø…µ√![]() ,
,
“ÚŒ™![]() £¨‘Úµ±
£¨‘Úµ±![]() π˝
π˝![]() ±£¨
±£¨![]() »°◊Ó¥Û£¨¥À ±
»°◊Ó¥Û£¨¥À ±![]()
º¥µ±![]() ±£¨¿˚»Û◊Ó¥Û£¨¥À ±
±£¨¿˚»Û◊Ó¥Û£¨¥À ±![]() .
.
π ¥∞∏Œ™:7£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥◊‹π´Àæ‘⁄A£¨B¡Ωµÿ∑÷±”–º◊°¢““¡Ω∏ˆœ¬ Ùπ´ÀæÕ¨÷÷–¬ƒ‹‘¥≤˙∆∑£®’‚¡Ω∏ˆπ´Àæ√øÃÏ∂ºπÃ∂®…˙≤˙50º˛≤˙∆∑£©£¨À˘…˙≤˙µƒ≤˙∆∑æ˘‘⁄±æµÿœ˙ €.≤˙∆∑Ω¯»À –≥°÷Æ«∞–Ë“™∂‘≤˙∆∑Ω¯–––‘ƒ‹ºÏ≤‚£¨µ√∑÷µÕ”⁄80∑÷µƒ∂®Œ™¥Œ∆∑£¨–Ë“™∑µ≥ß‘Ÿº”𧣪µ√∑÷≤ªµÕ”⁄80∑÷µƒ∂®Œ™’˝∆∑£¨ø…“‘Ω¯»À –≥°.ºÏ≤‚‘±Õ≥º∆¡Àº◊°¢““¡Ω∏ˆœ¬ Ùπ´Àæ100Ãϵƒ…˙≤˙«Èøˆº∞√øº˛≤˙∆∑”Ø¿˚ø˜À«Èøˆ£¨ ˝æ›»Á±ÌÀ˘ æ£∫
±Ì1
º◊π´Àæ | µ√∑÷ | [50£¨60£© | [60£¨70£© | [70£¨80£© | [80£¨90£© | [90£¨100] |
º˛ ˝ | 10 | 10 | 40 | 40 | 50 | |
ÃÏ ˝ | 10 | 10 | 10 | 10 | 80 |
±Ì2
º◊π´Àæ | µ√∑÷ | [50£¨60£© | [60£¨70£© | [70£¨80£© | [80£¨90£© | [90£¨100] |
º˛ ˝ | 10 | 5 | 40 | 45 | 50 | |
ÃÏ ˝ | 20 | 10 | 20 | 10 | 70 |
±Ì3
√øº˛’˝∆∑ | √øº˛¥Œ∆∑ | |
º◊π´Àæ | ”Ø2ÕÚ‘™ | ø˜3ÕÚ‘™ |
““π´Àæ | ”Ø3ÕÚ‘™ | ø˜3.5ÕÚ‘™ |
£®1£©∑÷±«Ûº◊°¢““¡Ω∏ˆπ´Àæ’‚100ÃÏ…˙≤˙µƒ≤˙∆∑µƒ’˝∆∑¬ £®”√∞Ÿ∑÷ ˝±Ì 棩.
£®2£© ‘Œ º◊°¢““¡Ω∏ˆπ´Àæ’‚100ÃÏ…˙≤˙µƒ≤˙∆∑µƒ◊‹¿˚»Ûƒƒ∏ˆ∏¸¥Û£øÀµ√˜¿Ì”….
£®3£©»Ù“‘º◊π´Àæ’‚100ÃÏ÷–√øÃÏ≤˙∆∑¿˚»Û◊‹∫Õ∂‘”¶µƒ∆µ¬ ◊˜Œ™∏≈¬ £¨¥”º◊π´Àæ’‚100ÃÏÀʪ˙≥È»°1ÃÏ£¨º«’‚ÃÏ≤˙∆∑¿˚»Û◊‹∫ÕŒ™X£¨«ÛXµƒ∑÷≤º¡–º∞∆‰ ˝—ß∆⁄Õ˚.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ªÃı∂´Œ˜¡˜œÚµƒ± ÷±∫”¡˜£¨œ÷¿˚”√∫Ω≈ƒŒfi»Àª˙![]() º‡øÿ∫”¡˜ƒœ∞∂œ‡æ‡150√◊µƒ
º‡øÿ∫”¡˜ƒœ∞∂œ‡æ‡150√◊µƒ![]()
![]() ¡Ωµ„¥¶£®
¡Ωµ„¥¶£®![]() ‘⁄
‘⁄![]() µƒ’˝Œ˜∑ΩœÚ£©£¨∫”¡˜±±∞∂µƒº‡øÿ÷––ƒ
µƒ’˝Œ˜∑ΩœÚ£©£¨∫”¡˜±±∞∂µƒº‡øÿ÷––ƒ![]() ‘⁄
‘⁄![]() µƒ’˝±±∑Ω100√◊¥¶£¨º‡øÿøÿ÷∆≥µ
µƒ’˝±±∑Ω100√◊¥¶£¨º‡øÿøÿ÷∆≥µ![]() ‘⁄
‘⁄![]() µƒ’˝Œ˜∑ΩœÚ£¨«“‘⁄Õ®œÚ
µƒ’˝Œ˜∑ΩœÚ£¨«“‘⁄Õ®œÚ![]() µƒ—ÿ∫”¬∑…œ‘À∂Ø£¨º‡øÿπ˝≥Ã÷–£¨±£÷§º‡øÿøÿ÷∆≥µ
µƒ—ÿ∫”¬∑…œ‘À∂Ø£¨º‡øÿπ˝≥Ã÷–£¨±£÷§º‡øÿøÿ÷∆≥µ![]() µΩŒfi»Àª˙
µΩŒfi»Àª˙![]() ∫ÕµΩº‡øÿ÷––ƒ
∫ÕµΩº‡øÿ÷––ƒ![]() µƒæ‡¿Î÷Æ∫Õ150√◊£¨∆Ω√Ê
µƒæ‡¿Î÷Æ∫Õ150√◊£¨∆Ω√Ê![]() º÷’¥π÷±”⁄ÀÆ∆Ω√Ê
º÷’¥π÷±”⁄ÀÆ∆Ω√Ê![]() £¨«“
£¨«“![]() £¨
£¨![]()
![]() ¡Ωµ„º‰æ‡¿ÎŒ¨≥÷‘⁄100√◊.
¡Ωµ„º‰æ‡¿ÎŒ¨≥÷‘⁄100√◊.
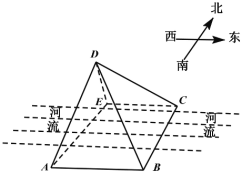
£®1£©µ±º‡øÿøÿ÷∆≥µ![]() µΩº‡øÿ÷––ƒ
µΩº‡øÿ÷––ƒ![]() µƒæ‡¿ÎŒ™100√◊ ±£¨«ÛŒfi»Àª˙
µƒæ‡¿ÎŒ™100√◊ ±£¨«ÛŒfi»Àª˙![]() 懿ÎÀÆ∆Ω√Ê
懿ÎÀÆ∆Ω√Ê![]() µƒæ‡¿Î£ª
µƒæ‡¿Î£ª
£®2£©»Ùº«Œfi»Àª˙![]() ø¥
ø¥![]() ¥¶µƒ∏©Ω«£®
¥¶µƒ∏©Ω«£®![]() £©£¨º‡øÿπ˝≥Ã÷–£¨Àƒ¿‚◊∂
£©£¨º‡øÿπ˝≥Ã÷–£¨Àƒ¿‚◊∂![]() ƒ⁄≤ø«¯”ÚµƒÃª˝Œ™º‡øÿ”∞œÏ«¯”Ú
ƒ⁄≤ø«¯”ÚµƒÃª˝Œ™º‡øÿ”∞œÏ«¯”Ú![]() £¨«ÎΩ´
£¨«ÎΩ´![]() ±Ì 挙πÿ”⁄
±Ì 挙πÿ”⁄![]() µƒ∫Ø ˝£¨≤¢«Û≥ˆº‡øÿ”∞œÏ«¯”Úµƒ◊Ó¥Û÷µ.
µƒ∫Ø ˝£¨≤¢«Û≥ˆº‡øÿ”∞œÏ«¯”Úµƒ◊Ó¥Û÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºπ˝≈◊ŒÔœfl![]() µƒΩπµ„
µƒΩπµ„![]() µƒ÷±œfl“¿¥ŒΩªíŌԜflº∞◊ºœfl”⁄µ„
µƒ÷±œfl“¿¥ŒΩªíŌԜflº∞◊ºœfl”⁄µ„![]() £¨»Ù
£¨»Ù![]() £¨«“
£¨«“![]() £¨‘Ú
£¨‘Ú![]() £® £©
£® £©
A.2B.![]() C.3D.6
C.3D.6
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨æÿ–Œ![]() ∫Õ¡‚–Œ
∫Õ¡‚–Œ![]() À˘‘⁄µƒ∆Ω√Êœ‡ª•¥π÷±£¨
À˘‘⁄µƒ∆Ω√Êœ‡ª•¥π÷±£¨![]() £¨
£¨![]() Œ™
Œ™![]() µƒ÷–µ„.
µƒ÷–µ„.

(¢Ò)«Û÷§£∫![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
(¢Ú) «Û![]() £¨
£¨![]() £¨«Û∂˛√ÊΩ«
£¨«Û∂˛√ÊΩ«![]() µƒ”‡œ“÷µ.
µƒ”‡œ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø ˝—ß÷–”––Ì∂‡–Œ◊¥”≈√¿‘¢“‚√¿∫√µƒ«˙œfl£¨«˙œfl![]() æÕ «∆‰÷–÷Æ“ª£®»ÁÕº£©£Æ∏¯≥ˆœ¬¡–»˝∏ˆΩ·¬€£∫
æÕ «∆‰÷–÷Æ“ª£®»ÁÕº£©£Æ∏¯≥ˆœ¬¡–»˝∏ˆΩ·¬€£∫

¢Ÿ«˙œfl![]() «°∫√æ≠π˝6∏ˆ’˚µ„£®º¥∫·◊›◊¯±Íæ˘Œ™’˚ ˝µƒµ„£©£ª
«°∫√æ≠π˝6∏ˆ’˚µ„£®º¥∫·◊›◊¯±Íæ˘Œ™’˚ ˝µƒµ„£©£ª
¢⁄«˙œfl![]() …œ¥Ê‘⁄µΩ‘≠µ„µƒæ‡¿Î≥¨π˝
…œ¥Ê‘⁄µΩ‘≠µ„µƒæ‡¿Î≥¨π˝![]() µƒµ„£ª
µƒµ„£ª
¢€«˙œfl![]() À˘Œß≥…µƒ°∞–ƒ–Œ°±«¯”Úµƒ√ʪ˝–°”⁄3£Æ
À˘Œß≥…µƒ°∞–ƒ–Œ°±«¯”Úµƒ√ʪ˝–°”⁄3£Æ
∆‰÷–£¨À˘”–¥ÌŒÛΩ·¬€µƒ–Ú∫≈ «______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÕ÷‘≤![]() µƒ”“Ωπµ„Œ™FµΩ÷±œfl
µƒ”“Ωπµ„Œ™FµΩ÷±œfl![]() µƒæ‡¿ÎŒ™
µƒæ‡¿ÎŒ™![]() £¨≈◊ŒÔœfl
£¨≈◊ŒÔœfl![]() µƒΩ𵄔ÎÕ÷‘≤EµƒΩπµ„F÷ÿ∫œ£¨π˝F◊˜”Îx÷·¥π÷±µƒ÷±œflΩªÕ÷‘≤”⁄S£¨T¡Ωµ„£¨Ωª≈◊ŒÔœfl”⁄C£¨D¡Ωµ„£¨«“
µƒΩ𵄔ÎÕ÷‘≤EµƒΩπµ„F÷ÿ∫œ£¨π˝F◊˜”Îx÷·¥π÷±µƒ÷±œflΩªÕ÷‘≤”⁄S£¨T¡Ωµ„£¨Ωª≈◊ŒÔœfl”⁄C£¨D¡Ωµ„£¨«“![]() £Æ
£Æ
£®1£©«ÛÕ÷‘≤Eº∞≈◊ŒÔœflGµƒ∑Ω≥Ã;
£®2£©π˝µ„F«“–±¬ Œ™kµƒ÷±œfllΩªÕ÷‘≤”⁄A£¨Bµ„£¨Ωª≈◊ŒÔœfl”⁄M£¨N¡Ωµ„£¨»ÁÕºÀ˘ 棨«ÎŒ «∑ҥʑ⁄ µ≥£ ˝![]() £¨ π
£¨ π![]() Œ™≥£ ˝£¨»Ù¥Ê‘⁄£¨«Û≥ˆ
Œ™≥£ ˝£¨»Ù¥Ê‘⁄£¨«Û≥ˆ![]() µƒ÷µ;»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
µƒ÷µ;»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ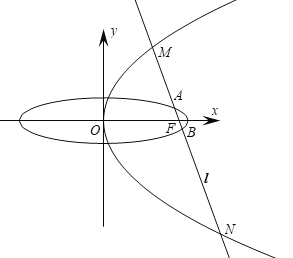
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë“‘![]() µƒ±fl
µƒ±fl![]() Œ™≥§÷·«“π˝µ„
Œ™≥§÷·«“π˝µ„![]() µƒÕ÷‘≤
µƒÕ÷‘≤![]() µƒ∑Ω≥ÃŒ™
µƒ∑Ω≥ÃŒ™![]() Õ÷‘≤
Õ÷‘≤![]() µƒ¿Î–ƒ¬
µƒ¿Î–ƒ¬ ![]() £¨
£¨![]() √ʪ˝µƒ◊Ó¥Û÷µŒ™
√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() £¨
£¨![]() ∫Õ
∫Õ![]() À˘‘⁄µƒ÷±œfl∑÷±”Î÷±œfl
À˘‘⁄µƒ÷±œfl∑÷±”Î÷±œfl![]() œ‡Ωª”⁄µ„
œ‡Ωª”⁄µ„![]() £¨
£¨![]() .
.
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë![]() ”Î
”Î![]() µƒÕ‚Ω”‘≤µƒ√ʪ˝∑÷±Œ™
µƒÕ‚Ω”‘≤µƒ√ʪ˝∑÷±Œ™![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ◊Ó–°÷µ.
µƒ◊Ó–°÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–![]() µƒ«∞nœÓ∫ÕŒ™
µƒ«∞nœÓ∫ÕŒ™![]() £¨∞—¬˙◊„Ãıº˛
£¨∞—¬˙◊„Ãıº˛![]()
![]() µƒÀ˘”– ˝¡–
µƒÀ˘”– ˝¡–![]() ππ≥…µƒºØ∫œº«Œ™
ππ≥…µƒºØ∫œº«Œ™![]() £Æ
£Æ
£®1£©»Ù ˝¡–![]() µƒÕ®œÓŒ™
µƒÕ®œÓŒ™![]() £¨‘Ú
£¨‘Ú![]() «∑Ò Ù”⁄
«∑Ò Ù”⁄![]() £ø
£ø
£®2£©»Ù ˝¡–![]() «µ»≤Ó ˝¡–£¨«“
«µ»≤Ó ˝¡–£¨«“![]() £¨«Û
£¨«Û![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®3£©»Ù ˝¡–![]() µƒ∏˜œÓæ˘Œ™’˝ ˝£¨«“
µƒ∏˜œÓæ˘Œ™’˝ ˝£¨«“![]() £¨ ˝¡–
£¨ ˝¡–![]() ÷– «∑ҥʑ⁄Œfi«Ó∂‡œÓ“¿¥Œ≥…µ»≤Ó ˝¡–£¨»Ù¥Ê‘⁄£¨∏¯≥ˆ“ª∏ˆ ˝¡–
÷– «∑ҥʑ⁄Œfi«Ó∂‡œÓ“¿¥Œ≥…µ»≤Ó ˝¡–£¨»Ù¥Ê‘⁄£¨∏¯≥ˆ“ª∏ˆ ˝¡–![]() µƒÕ®œÓ£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
µƒÕ®œÓ£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com