[题目]已知△ABC中.AC= .BC= .△ABC的面积为 .若线段BA的延长线上存在点D.使∠BDC= .则CD= ．题目和参考答案——青夏教育精英家教网—

【题目】已知△ABC中，AC= ，BC= ，△ABC的面积为，若线段BA的延长线上存在点D，使∠BDC= ，则CD= ．

【答案】
【解析】解：∵AC= ，BC= ，△ABC的面积为 = ACBCsin∠ACB= sin∠ACB， ∴sin∠ACB= ，
∴∠ACB= ，或，
∵若∠ACB= ，∠BDC= ＜∠BAC，可得：∠BAC+∠ACB＞ + ＞π，与三角形内角和定理矛盾，
∴∠ACB= ，
∴在△ABC中，由余弦定理可得：AB= ，
∴∠B= ，
∴在△BCD中，由正弦定理可得：CD= ．
所以答案是：．

【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:．

练习册系列答案

暑假作业暑假快乐练西安出版社系列答案

德华书业暑假训练营学年总复习安徽文艺出版社系列答案

金牌作业本南方教与学系列答案

宏翔文化暑假一本通期末加暑假加预习系列答案

龙人图书快乐假期暑假作业郑州大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF 2CE，G是线段BF上一点，AB=AF=BC．
（Ⅰ）若EG∥平面ABC，求的值；
（Ⅱ）求二面角A﹣BF﹣E的大小的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂拟生产甲、乙两种实销产品．已知每件甲产品的利润为0.4万元，每件乙产品的利润为0.3万元，两种产品都需要在A，B两种设备上加工，且加工一件甲、乙产品在A，B设备上所需工时（单位：h）分别如表所示．

	甲产品所需工时	乙产品所需工时
A设备	2	3
B设备	4	1

若A设备每月的工时限额为400h，B设备每月的工时限额为300h，则该厂每月生产甲、乙两种产品可获得的最大利润为（）
A.40万元
B.45万元
C.50万元
D.55万元

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】[选修4-4：坐标系与参数方程]
在直角坐标系xOy中，双曲线E的参数方程为（θ为参数），设E的右焦点为F，经过第一象限的渐进线为l．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．
（1）求直线l的极坐标方程；
（2）设过F与l垂直的直线与y轴相交于点A，P是l上异于原点O的点，当A，O，F，P四点在同一圆上时，求这个圆的极坐标方程及点P的极坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司计划购买1台机器，该种机器使用三年后即被淘汰.机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元. 在机器使用期间，如果备件不足再购买，则每个500元.现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：

记x表示1台机器在三年使用期内需更换的易损零件数，y表示1台机器在购买易损零件上所需的费用（单位：元），表示购机的同时购买的易损零件数.

（1）若=19，求y与x的函数解析式；

（2）若要求“需更换的易损零件数不大于”的频率不小于0.8，求的最小值；

（3）假设这100台机器在购机的同时每台都购买18个易损零件，或每台都购买19个易损零件，分别计算这100台机器在购买易损零件上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买18个还是19个易损零件？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图1，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，G为BD中点，点R在线段BH上，且 =λ（λ＞0）．现将△AED，△CFD，△DEF分别沿DE，DF，EF折起，使点A，C重合于点B（该点记为P），如图2所示．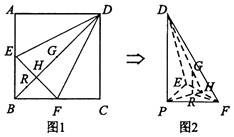

（I）若λ=2，求证：GR⊥平面PEF；
（Ⅱ）是否存在正实数λ，使得直线FR与平面DEF所成角的正弦值为？若存在，求出λ的值；若不存在，请说明理由．