
已知z="2x"
+y,x,y满足 且z的最大值是最小值的4倍,则a的值是 .
且z的最大值是最小值的4倍,则a的值是 .
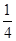
【解析】
试题分析:题意可得先作出不等式表示的 平面区域,由z=2x+y可得y=-2x+z,则z表示直线y=-2x+z在y轴上的截距,截距越大,z越大,可求Z的最大值与最小值,即可求解a
由题意可得,B(1,1)
∴a<1,不等式组表示的 平面区域如图所示的△ABC
由z=2x+y可得y=-2x+z,则z表示直线y=-2x+z在y轴上的截距,截距越大,z越大
作直线L:y=-2x,把直线向可行域平移,当直线经过C时Z最小,当直线经过点B时,Z最大,由x=a,y=x,解得交点(a,a),此时Z=3a
由y=x,x+y-2=0,可得交点为B(1,1),此时z=3,故可知∴3=4×3a
∴a=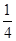 故答案
故答案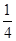
考点:线性规划的最优解问题
点评:线性规划是高考重要内容,也是常考内容.此题考查该知识点增加一点变化,比较好.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014届福建省三明市高二下学期第一次阶段考试文数(解析版) 题型:解答题
(1)已知复数z="(2+i)(i-3)+4-2i;" 求复数z的共轭复数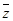 及|
及|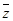 |;
|;
(2)设复数z1=(a2-2a)+ai是纯虚数,求实数a的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
已知M 是△ABC内的一点(不含边界),且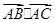 ="
2"
="
2" 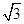 , ∠BAC =30°,若△MBC,△MCA和△MAB的面积分别为x,y,z,记f(x,y,z)=
, ∠BAC =30°,若△MBC,△MCA和△MAB的面积分别为x,y,z,记f(x,y,z)=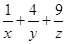 ,则f(x,y,z)的最小值是__
,则f(x,y,z)的最小值是__
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com