
【题目】已知函数![]()
![]() 的
的
部分图像如图所示.
(Ⅰ)求函数![]() 的解析式及
的解析式及![]() 图像的对称轴方程;
图像的对称轴方程;
(Ⅱ)把函数![]() 图像上点的横坐标扩大到原来的
图像上点的横坐标扩大到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移
![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求关于
的图象,求关于![]() 的方程
的方程![]()
在![]() 时所有的实数根之和.
时所有的实数根之和.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据环境保护部《环境空气质量指数(![]() )技术规定》,空气质量指数(
)技术规定》,空气质量指数(![]() )在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
)在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
某城市空气质量监测部门对近300天空气中![]() 浓度进行统计,得出这300天
浓度进行统计,得出这300天![]() 浓度的频率分布直方图如图,将
浓度的频率分布直方图如图,将![]() 浓度落入各组的频率视为概率,并假设每天的
浓度落入各组的频率视为概率,并假设每天的![]() 浓度相互独立.
浓度相互独立.
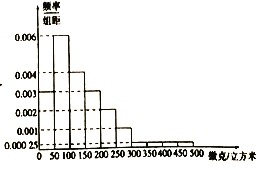
(1)求当地监测部门发布颜色预警的概率;
(2)据当地监测站数据显示未来4天将出现3天严重污染,求监测部门发布红色预警的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的一段图象如图所示
)的一段图象如图所示 
(1)求f(x)的解析式;
(2)把f(x)的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com