
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

【答案】(1)0.02;(2)75;(3)0.4
【解析】
(1)由面积和为1,可解得x的值;
(2)由中位数两侧的面积相等,可解得中位数;
(3)列出所有基本事件共10个,其中符合条件的共4个,从而可以解出所求概率.
解:(1)由(0.005+0.010+0.030+0.025+0.010+x)×10=1,解得x=0.02.
(2)中位数设为m,则0.05+0.1+0.2+(m-70)×0.03=0.5,解得m=75.
(3)可得满意度评分值在[60,70)内有20人,抽得样本为2人,记为a1,a2
满意度评分值在[70,80)内有30人,抽得样本为3人,记为b1,b2,b3,
记“5人中随机抽取2人作主题发言,抽出的2人恰在同一组”为事件A,
基本事件有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),
(a2,b3),(b1,b2),(b1,b3),(b2,b3)共10个,A包含的基本事件个数为4个,
利用古典概型概率公式可知P(A)=0.4.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E为PB的中点。
,∠ABC=∠BCD=90°,E为PB的中点。

(1)证明:CE∥面PAD.
(2)若直线CE与底面ABCD所成的角为45°,求四棱锥P-ABCD的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: ![]() ,过点
,过点![]() 的直线l的参数方程为:
的直线l的参数方程为: 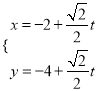 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若|PM |,|MN|,|PN|成等比数列,求a的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得弦
轴上截得弦![]() 的长为4。
的长为4。
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)设![]() ,过点
,过点![]() 斜率为
斜率为![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点, ![]() 的延长线交轨迹
的延长线交轨迹![]() 于
于![]() 两点。
两点。
①若![]() 的面积为3,求
的面积为3,求![]() 的值。
的值。
②记直线![]() 的斜率为
的斜率为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值。
为定值,并求出这个定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实中央省市关于新型冠状病毒肺炎疫情防控工作要求,积极应对新型冠状病毒疫情,切实做好2020年春季开学工作,保障校园安全稳定,普及防控知识,确保师生生命安全和身体健康.某校开学前,组织高三年级800名学生参加了“疫情防控”网络知识竞赛(满分150分).已知这800名学生的成绩均不低于90分,将这800名学生的成绩分组如下:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,第六组
,第六组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
的值并估计这800名学生的平均成绩(同一组中的数据用该组区间的中点值代表);
(2)该校“群防群控”督查组为更好地督促高三学生的“个人防控”,准备从这800名学生中取2名学生参与督查工作,其取办法是:先在第二组第五组第六组中用分层抽样的方法抽取6名学生,再从这6名学生中随机抽取2名学生.记这2名学生的竞赛成绩分别为![]()
![]() .求事件
.求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com