
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取2000名进行调查,将受访用户按年龄分成5组: ![]() 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图:

(1)求![]() 的值;
的值;
(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄.
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.

(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市每年春节前后,由于大量的烟花炮竹的燃放,空气污染较为严重.该市环保研究所对近年春节前后每天的空气污染情况调查研究后发现,每天空气污染的指数![]() 随时刻
随时刻![]() (时)变化的规律满足表达式
(时)变化的规律满足表达式![]() ,
,![]() ,其中
,其中![]() 为空气治理调节参数,且
为空气治理调节参数,且![]() .
.
(1)令![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若规定每天中![]() 的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数
的最大值作为当天的空气污染指数,要使该市每天的空气污染指数不超过5,试求调节参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线l:(m+3)x-(m+2)y+m=0与圆C:(x-3)2+(y-4)2=9.
(1)求证:无论m为何值,直线l总过定点A,并说明直线l与圆C总相交.
(2)m为何值时,直线l被圆C所截得的弦长最小?请求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
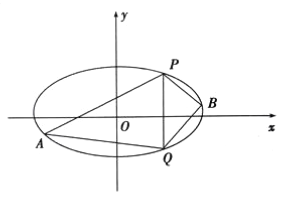
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下面两个的相关命题的逆命题、否命题、逆否命题,并判断它们的真假:
(1)命题:若![]() ,则
,则![]() .
.
逆命题:_______________________________________________________(________)
逆否命题:_____________________________________________________(________)
(2)命题:设![]() 是实数,如果
是实数,如果![]() ,那么
,那么![]() 有实数根。
有实数根。
否命题:_______________________________________________________(________)
逆否命题:_____________________________________________________(________)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,
,
(1)求该椭圆的标准方程;
(2)(文)若![]() 是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
是椭圆上的动点,过P作垂直于x轴的垂线,垂足为M,延长MP至N,使得P恰好为MN中点,求点N的轨迹方程;
(理)若已知点![]() ,
,![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
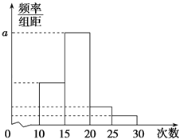
(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com