
分析 根据$\overrightarrow{BD}$=λ($\frac{\overrightarrow{BA}}{|\overrightarrow{BA|}sinA}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC|}sinC}$),容易判断点D为AC的中点,由三角形的中线长定理和余弦定理,可得AC,BC的长,再由正弦定理,可得sinA.
解答 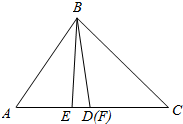 解:如图,过B作BE⊥AC,垂足为E,取AC中点F,连接BF,
解:如图,过B作BE⊥AC,垂足为E,取AC中点F,连接BF,
则$\overrightarrow{BD}$=λ($\frac{\overrightarrow{BA}}{|\overrightarrow{BA|}sinA}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC|}sinC}$)(λ>0)
=λ($\frac{\overrightarrow{BA}}{|\overrightarrow{BE}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BE}|}$)=$\frac{2λ\overrightarrow{BF}}{|\overrightarrow{BE}|}$;
∴$\overrightarrow{BD}$和$\overrightarrow{BF}$共线,∴D点和F点重合,∴D是AC的中点,
由中线长定理可得,BD=$\frac{1}{2}$$\sqrt{2A{B}^{2}+2B{C}^{2}-A{C}^{2}}$=$\frac{1}{2}$$\sqrt{\frac{64}{3}+2B{C}^{2}-A{C}^{2}}$=$\sqrt{5}$,
又AC2=AB2+BC2-2AB•BC•cosB,即为AC2=$\frac{32}{3}$+BC2-$\frac{8\sqrt{6}}{3}$•BC•$\frac{\sqrt{6}}{6}$,
解方程可得BC=2,AC=$\frac{2\sqrt{21}}{3}$,
由正弦定理可得$\frac{BC}{sinA}$=$\frac{AC}{sinB}$,可得sinA=$\frac{BC•sinB}{AC}$=$\frac{2×\frac{\sqrt{30}}{6}}{\frac{2\sqrt{21}}{3}}$=$\frac{\sqrt{70}}{14}$.
故答案为:$\frac{\sqrt{70}}{14}$.
点评 本题考查向量加法的平行四边形法则,共线向量基本定理,余弦定理的运用,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
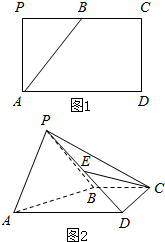 如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.
如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
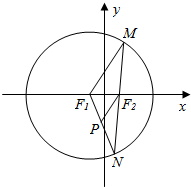 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com