
【题目】已知数列{an}中,a1=1,a2= ![]() ,且an+1=
,且an+1= ![]() (n=2,3,4…).
(n=2,3,4…).
(1)求数列{an}的通项公式;
(2)求证:对一切n∈N* , 有 ![]() <
< ![]() .
.
【答案】
(1)解:∵a1=1,a2= ![]() ,且an+1=
,且an+1= ![]() (nkkk=2,3,4…),
(nkkk=2,3,4…),
∴当n≥2时, ![]() =
= ![]() ,
,
两边同时除以n,得 ![]() ,
,
∴ ![]() =﹣(
=﹣( ![]() ),
),
∴ ![]() =﹣
=﹣ ![]() =﹣(1﹣
=﹣(1﹣ ![]() )
)
∴ ![]() =﹣(1﹣
=﹣(1﹣ ![]() ),n≥2,
),n≥2,
∴ ![]() ,
,
∴an= ![]() ,n≥2,
,n≥2,
当n=1时,上式成立,
∴an= ![]() ,n∈N*
,n∈N*
(2)证明:当k≥2时, ![]() =
= ![]() ,
,
∴当n≥2时,
![]() =1+
=1+ ![]() <1+
<1+ ![]() [(
[( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )]
)]
=1+ ![]() <1+
<1+ ![]() =
= ![]() ,
,
又n=1时, ![]() ,
,
∴对一切n∈N*,有 ![]() ak2<
ak2< ![]()
【解析】(1)当n≥2时, ![]() =
= ![]() ,从而
,从而 ![]() =﹣(
=﹣( ![]() ),进而得到
),进而得到 ![]() =﹣(1﹣
=﹣(1﹣ ![]() ),由此能求出an=
),由此能求出an= ![]() ,n∈N* . (2)当k≥2时,
,n∈N* . (2)当k≥2时, ![]() =
= ![]() ,由此利用裂项求和法能证明对一切n∈N* , 有
,由此利用裂项求和法能证明对一切n∈N* , 有 ![]() <
< ![]() .
.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(Ⅱ)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC,已知PA⊥面ABC,AD⊥BC于D,BC=CD=AD=1,设PD=x,∠BPC=θ,记函数f(x)=tanθ,则下列表述正确的是( ) 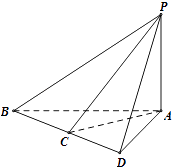
A.f(x)是关于x的增函数
B.f(x)是关于x的减函数
C.f(x)关于x先递增后递减
D.关于x先递减后递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,且点P为AD的中点,点Q为SB的中点.
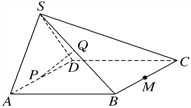
(1)求证:CD⊥平面SAD.
(2)求证:PQ∥平面SCD.
(3)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且A,B,C成等差数列
(1)若b=2 ![]() ,c=2,求△ABC的面积;
,c=2,求△ABC的面积;
(2)若a,b,c成等比数列,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用水,实行“阶梯式”水价,将该市每户居民的月用水量划分为三档:月用水量不超过4吨的部分按2元/吨收费,超过4吨但不超过8吨的部分按4元/吨收费,超过8吨的部分按8元/吨收费.

(1)求居民月用水量费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:吨)的函数解析式;
(单位:吨)的函数解析式;
(2)为了了解居民的用水情况,通过抽样,获得今年3月份100户居民每户的用水量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年3月份用水费用不超过16元的占66%,求![]() 的值;
的值;
(3)在满足条件(2)的条件下,若以这100户居民用水量的频率代替该月全市居民用户用水量的概率.且同组中的数据用该组区间的中点值代替.记为该市居民用户3月份的用水费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com