
【题目】设![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的两个焦点,过
的两个焦点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 在
在![]() 轴上方),则四边形
轴上方),则四边形![]() 面积的最大值为__________.
面积的最大值为__________.
科目:高中数学 来源: 题型:
【题目】某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表1所示:
表1:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 6 | 11 | 21 | 34 | 66 | 101 | 196 |
根据以上数据,绘制了散点图.
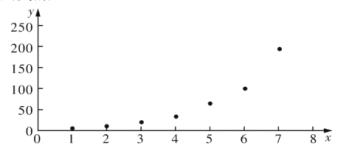
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为扫码支付的人次
均为大于零的常数)哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据(1)的判断结果及表1中的数据,建立![]() 关于
关于![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次.
的回归方程,并预测活动推出第8天使用扫码支付的人次.
(3)推广期结束后,为更好的服务乘客,车队随机调查了100人次的乘车支付方式,得到如下结果:
表2
支付方式 | 现金 | 乘车卡 | 扫码 |
人次 | 10 | 60 | 30 |
已知该线路公交车票价2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据调査结果发现:使用扫码支付的乘客中有5名乘客享受7折优惠,有10名乘客享受8折优惠,有15名乘客享受9折优惠.预计该车队每辆车每个月有1万人次乘车,根据所给数据,以事件发生的频率作为相应事件发生的概率,在不考虑其他因素的条件下,按照上述收费标准,试估计该车队一辆车一年的总收入.
参考数据:
|
|
|
|
|
62.14 | 1.54 | 2535 | 50.12 | 3.47 |
其中![]() .
.
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: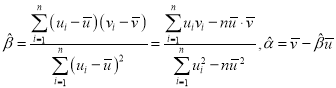 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁超市旗舰店在元旦当天推出一个购物满百元抽奖活动,凡是一次性购物满百元者可以从抽奖箱中一次性任意摸出2个小球(抽奖箱内共有5个小球,每个小球大小形状完全相同,这5个小球上分别标有1,2,3,4,5 这5个数字).
(1)列出摸出的2个小球的所有可能的结果.
(2)已知该超市活动规定:摸出的2个小球都是偶数为一等奖;摸出的2个小球都是奇数为二等奖.请分别求获得一等奖的概率与获得二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三棱锥![]() 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等,![]() 是棱
是棱![]() 上的点(不含端点),记直线
上的点(不含端点),记直线![]() 与直线
与直线![]() 所成角为
所成角为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)若线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若![]() 的斜率为
的斜率为![]() ,且
,且![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中医药研究所研制出一种新型抗癌药物,服用后需要检验血液是否为阳性,现有![]() 份血液样本每个样本取到的可能性均等,有以下两种检验方式:(1)逐份检验,则需要检验
份血液样本每个样本取到的可能性均等,有以下两种检验方式:(1)逐份检验,则需要检验![]() 次;(2)混合检验,将其中
次;(2)混合检验,将其中![]() 份血液样本分别取样混合在一起检验,若结果为阴性,则这
份血液样本分别取样混合在一起检验,若结果为阴性,则这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只需检验一次就够了;若检验结果为阳性,为了明确这
份血液样本只需检验一次就够了;若检验结果为阳性,为了明确这![]() 份血液究竟哪份为阳性,就需要对这
份血液究竟哪份为阳性,就需要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次假设在接受检验的血液样本中,每份样本的检验结果总阳性还是阴性都是相互独立的,且每份样本是阳性的概率为
次假设在接受检验的血液样本中,每份样本的检验结果总阳性还是阴性都是相互独立的,且每份样本是阳性的概率为![]() .
.
(1)假设有6份血液样本,其中只有两份样本为阳性,若采取遂份检验的方式,求恰好经过两次检验就能把阳性样本全部检验出来的概率.
(2)现取其中的![]() 份血液样本,记采用逐份检验的方式,样本需要检验的次数为
份血液样本,记采用逐份检验的方式,样本需要检验的次数为![]() ;采用混合检验的方式,样本简要检验的总次数为
;采用混合检验的方式,样本简要检验的总次数为![]() ;
;
(ⅰ)若![]() ,试运用概率与统计的知识,求
,试运用概率与统计的知识,求![]() 关于
关于![]() 的函数关系
的函数关系![]() ,
,
(ⅱ)若![]() ,采用混合检验的方式需要检验的总次数的期望比逐份检验的总次数的期望少,求
,采用混合检验的方式需要检验的总次数的期望比逐份检验的总次数的期望少,求![]() 的最大值(
的最大值(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季受新冠肺炎疫情的影响,利用网络软件办公与学习成为了一种新的生活方式,网上办公软件的开发与使用成为了一个热门话题.为了解“钉钉”软件的使用情况,“钉钉”公司借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
35岁及以下 | 70 | 30 | 100 |
35岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关?
(2)现从所抽取的35岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用“钉钉”软件的概率.
参考公式: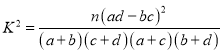 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天然气已经进入了千家万户,某市政府为了对天然气的使用进行科学管理,节约气资源,计划确定一个家庭年用量的标准.为此,对全市家庭日常用气的情况进行抽样调查,获得了部分家庭某年的用气量(单位:立方米).将统计结果绘制成下面的频率分布直方图(如图所示).由于操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.若以各组区间中点值代表该组的取值,则估计全市家庭年均用气量约为( )
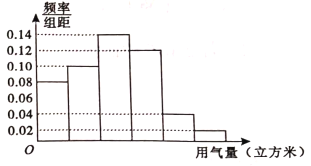
A.6.5立方米B.5立方米C.4.5立方米D.2.5立方米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com