练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某公司为了对一种新产品进行合理定价，将该产品按亊先拟定的价格进行试销，得到如下数据：

    单价x（元）

    4

    5

    6

    7

    8

    9

    销量V（件）

    90

    84

    83

    80

    75

    68

    由表中数据．求得线性回归方程为 =﹣4x+a．若在这些样本点中任取一点，則它在回归直线右上方的概率为
    （ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解： = （4+5+6+7+8+9）= ， = （90+84+83+80+75+68）=80 ∵ =﹣4x+a，
    ∴a=106，
    ∴回归直线方程 =﹣4x+106；
    数据（4，90），（5，84），（6，83），（7，80），（8，75），（9，68）．
    6个点中有3个点在直线右上方，即（6，83），（7，80），（8，75）．
    其这些样本点中任取1点，共有6种不同的取法，
    故这点恰好在回归直线右上方的概率P= = ．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】阅读如图的程序框图，运行相应的程序，则输出的S值为（ ）

    A.2
    B.3
    C.4
    D.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C1的参数方程为 ，曲线C2的极坐标方程为 ．
    （1）求曲线C1的普通方程和曲线C2的直角坐标方程；
    （2）设P为曲线C1上一点，Q曲线C2上一点，求|PQ|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sinxcosx﹣sin2x﹣3cos2x+1．
    （1）求函数y=f（x）的单调递增区间；
    （2）若函数y=f（x）在区间[0，a]上恰有3个零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= sin2x+cos2x．
    （1）当x∈[0， ]时，求f（x）的取值范围；
    （2）求函数y=f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了检测某种产品的质量（单位：千克），抽取了一个容量为N的样本，整理得到的数据作出了频率分布表和频率分布直方图如图：

    分组

    频数

    频率

    [17.5，20）

    10

    0.05

    [20，225）

    50

    0.25

    [22.5，25）

    a

    b

    [25，27.5）

    40

    c

    [27.5，30]

    20

    0.10

    合计

    N

    1

    （Ⅰ）求出表中N及a，b，c的值；
    （Ⅱ）求频率分布直方图中d的值；
    （Ⅲ）从该产品中随机抽取一件，试估计这件产品的质量少于25千克的概率．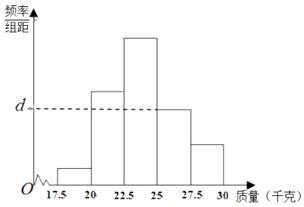

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题：“x∈{x|﹣1＜x＜1}，使等式x2﹣x﹣m=0成立”是真命题．
    （1）求实数m的取值集合M；
    （2）设不等式 的解集为N，若x∈N是x∈M的必要不充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知锐角△ABC的三个内角A，B，C的对边分别为a，b，c，且 =（a，b+c）， ．
    （1）求角A；
    （2）若a=3，求△ABC面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图四棱锥E﹣ABCD中，四边形ABCD为平行四边形，△BCE为等边三角形，△ABE是以∠A为直角的等腰直角三角形，且AC=BC． （Ⅰ）证明：平面ABE⊥平面BCE；
    （Ⅱ）求二面角A﹣DE﹣C的余弦值．

    查看答案和解析>>

    同步练习册答案