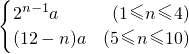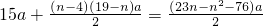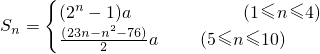Question

某城市决定对城区住房进行改造，在建新住房的同时拆除部分旧住房．第一年建新住房am²，第二年到第四年，每年建设的新住房比前一年增长100%，从第五年起，每年建设的新住房都比前一年减少 am²；已知旧住房总面积为32am²，每年拆除的数量相同．
（Ⅰ）若10年后该城市住房总面积正好比改造前的住房总面积翻一番，则每年拆除的旧住房面积是多少m²？
（Ⅱ），求前n（1≤n≤10且n∈N）年新建住房总面积S_n

Answer 1

解：（I）10年后新建住房总面积为a+2a+4a+8a+7a+6a+5a+4a+3a+2a=42a．
设每年拆除的旧住房为xm²，则42a+（32a-10x）=2×32a，
解得x=a，即每年拆除的旧住房面积是am²
（Ⅱ）设第n年新建住房面积为a，则a_n=
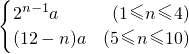
所以当1≤n≤4时，S_n=（2ⁿ-1）a；
当5≤n≤10时，S_n=a+2a+4a+8a+7a+6a+（12-n）a=
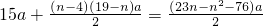
故
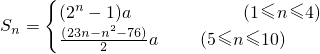
分析：（I）分别计算出10年后新建住房总面积，再设每年拆除的旧住房为xm²，列方程即可求得每年拆除的旧住房面积数；
（Ⅱ）先设第n年新建住房面积为a，分类讨论：当1≤n≤4时，当5≤n≤10时，分别求出新建住房总面积即可．
点评：本小题主要考查函数模型的选择与应用，属于基础题．解决实际问题通常有四个步骤：（1）阅读理解，认真审题；（2）引进数学符号，建立数学模型；（3）利用数学的方法，得到数学结果；（4）转译成具体问题作出解答，其中关键是建立数学模型．