
【题目】已知函数![]()
![]() 的最大值是0,函数
的最大值是0,函数![]()
![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求出函数的导函数,根据函数的单调性求出f(x)的最大值,得到关于m的方程,进而求出m的值;
(Ⅱ)构造函数F(x)=f(x)-g(x),求出函数的导函数![]() ,进而求出
,进而求出![]() 的导函数
的导函数![]() ,利用导数与函数单调性的关系,通过讨论a的范围,得到函数的单调区间,结合函数恒成立问题,进而求出a的取值范围.
,利用导数与函数单调性的关系,通过讨论a的范围,得到函数的单调区间,结合函数恒成立问题,进而求出a的取值范围.
(Ⅰ)函数![]() 的定义域为
的定义域为![]()
![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
令![]() ,得
,得![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减;
单调递减;
所以,当![]() 时,
时,![]() =
=![]()
于是,![]() ,得
,得![]() ,
,
易知,函数![]() 在
在![]() 处有唯一零点,所以
处有唯一零点,所以![]() ,
,![]() .
.
(Ⅱ)令![]() ,
,![]()
则![]() ,
,
设![]()
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
则![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
故当![]() 时,
时,![]() ,与已知矛盾.
,与已知矛盾.
②当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
则![]() 时,
时,![]()
故![]() 在
在![]() 上单调递减,
上单调递减,
则当![]() 时,
时,![]() ,与已知矛盾.
,与已知矛盾.
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增,故当
上单调递增,故当![]() 时,
时,![]() 恒成立.
恒成立.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
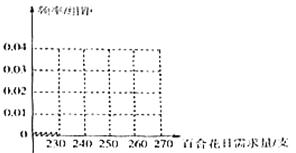
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() (a为正常数)与
(a为正常数)与![]() 在x轴上方仅有一个公共点P.
在x轴上方仅有一个公共点P.
(1)求实数m的取值范围(用a表示);
(2)O为原点,若![]() 与x轴的负半轴交于点A,当
与x轴的负半轴交于点A,当![]() 时,试求△OAP的面积的最大值(用a表示).
时,试求△OAP的面积的最大值(用a表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
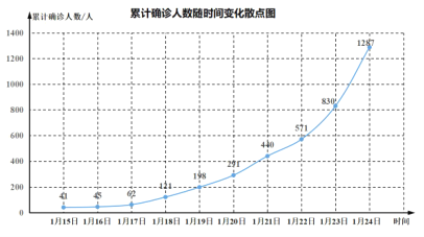
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为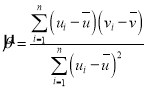 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究公司为了调查公众对某事件的关注程度,在某年的连续6个月内,月份![]() 和关注人数
和关注人数![]() (单位:百)(
(单位:百)(![]() )数据做了初步处理,得到下面的散点图及一些统计量的值.
)数据做了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
17.5 | 35 | 36.5 |
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明,并建立y关于x的回归方程;
(2)经统计,调查材料费用v(单位:百元)与调查人数满足函数关系![]() ,求材料费用的最小值,并预测此时的调查人数;
,求材料费用的最小值,并预测此时的调查人数;
(3)现从这6个月中,随机抽取3个月份,求关注人数不低于1600人的月份个数![]() 分布列与数学期望.
分布列与数学期望.
参考公式:相关系数 ,若
,若![]() ,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程组,解出即可;
的方程组,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用导数研究其单调性可得
, 利用导数研究其单调性可得
![]() ,
,
从而证明![]() .
.
试题解析:((1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;且
单调递增;且![]() ,
,
所以![]() 在
在![]() 上当单调递减,在
上当单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
故![]() ,
,
故![]() .
.
【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com