
ij�ؽ�������о���ס�����Ϊ m2��������Ҫ����ľɷ����ռ��һ�룬�����йز��ž���ÿ���Ե������ס�������10%��ס�������ʽ�����ס����ͬʱÿ����xm2�ľ�ס������֪�õ����˿���������Ϊ4.9�룮
m2��������Ҫ����ľɷ����ռ��һ�룬�����йز��ž���ÿ���Ե������ס�������10%��ס�������ʽ�����ס����ͬʱÿ����xm2�ľ�ס������֪�õ����˿���������Ϊ4.9�룮
��1�����10���õ������˾�ס��������ñ�Ŀǰ��һ������ôÿ��Ӧ����ľ�ס�����x�Ƕ��٣�
��2�����գ�1�����ٶȣ�����������ܲ��������Ҫ����ľɷ���
�������ݹ�����ʱ�ο���
| 1.19=2.38 | 1.00499=1.04 |
| 1.110=2.6 | 1.004910=1.05 |
| 1.111=2.85 | 1.004911=1.06 |
��1�� ����2�����16����ܲ��������Ҫ����ľɷ�.
����2�����16����ܲ��������Ҫ����ľɷ�.
���������������1���������������˿�Ϊ �ˣ���
�ˣ��� ����˿�Ϊ
����˿�Ϊ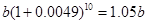 ������д��
������д�� ����ס�����Ϊ
����ס�����Ϊ ��
�� ����ס�����Ϊ
����ס�����Ϊ ��
�� ����ס�����Ϊ
����ס�����Ϊ ��
��
�ɴ˿����Ʋ� ����ס�����Ϊ
����ס�����Ϊ ��
��
���������˾�ס��������ñ�Ŀǰ��һ�������г����� ���Ӷ����
���Ӷ���� ����2���ɣ�1���ɵã�ÿ������ס�����Ϊ
����2���ɣ�1���ɵã�ÿ������ס�����Ϊ ���Ӷ�����������Ҫ����ľɷ����ռ��һ�룬��֪���������Ҫ����ľɷ���Ҫ��ʱ��Ϊ
���Ӷ�����������Ҫ����ľɷ����ռ��һ�룬��֪���������Ҫ����ľɷ���Ҫ��ʱ��Ϊ ��.
��.
��1��������˿�Ϊ �ˣ���
�ˣ��� ����˿�Ϊ
����˿�Ϊ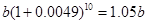 3��
3�� ����ס�����Ϊ
����ס�����Ϊ ��
�� ����ס�����Ϊ
����ס�����Ϊ ��
�� ����ס�����Ϊ
����ס�����Ϊ ��
��
�� ����ס�����Ϊ
����ס�����Ϊ .........8��
.........8��
�� 12��
12��
�� �� 13��
�� 13��
(2)�ɣ�1���ɵ�ȫ������ɷ����� �꣬
�꣬
�����16����ܲ��������Ҫ����ľɷ�.......... 16�֣�
���㣺���е��ۺ�����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���������ĵȱ�����{an}����a1+a2+a3=14����a2+1��a1��a3�ĵȲ����
��1��������{an}��ͨ�ʽ��
��2����bn=anlog2an��������{bn}��ǰn���Sn��
��3��������n��N*��ʹ��Sn+1��2��8n3�˳�������ʵ���˵���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪��Բ �����Ҷ���ֱ���
�����Ҷ���ֱ���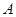 ��
�� �����ҽ���ֱ���
�����ҽ���ֱ��� ��
�� ����
���� ��
�� ��
�� �ɵȱ����У������Բ�������ʣ�
�ɵȱ����У������Բ�������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪�Ȳ�����{an}������a1��1������d>0���ҵ�2���5���14��ֱ�Ϊ�ȱ�����{bn}�ĵ�2���3���4�
(1)������{an}��{bn}��ͨ�ʽ��
(2)������{cn}��n��N*������ ��
�� ������
������ ��an��1��������c1��c2��c3������c2014��ֵ��
��an��1��������c1��c2��c3������c2014��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
���� ��
�У� ��ǰ
��ǰ ��ĺ���
���� ����
���� ��
�� .
.
��1����� 
��2�������� ��ͨ�ʽ��
��ͨ�ʽ��
��3����֤�� .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ס����������зֱ�ʢ������Ũ�ȵ�ij����Һ ���Ӽ�������ȡ��
���Ӽ�������ȡ�� ��Һ�����䵹���������н��ȣ��ٴ���������ȡ��
��Һ�����䵹���������н��ȣ��ٴ���������ȡ�� ��Һ�����䵹��������н��ȣ����Ϊ��һ�ε��ͣ���֪��һ�ε��ͺס���������Һ��Ũ�ȷֱ��Ϊ��
��Һ�����䵹��������н��ȣ����Ϊ��һ�ε��ͣ���֪��һ�ε��ͺס���������Һ��Ũ�ȷֱ��Ϊ�� ��
�� ����
���� �ε��ͺ�ļס���������Һ��Ũ�ȷֱ��Ϊ��
�ε��ͺ�ļס���������Һ��Ũ�ȷֱ��Ϊ�� ��
�� .
.
��1������ ��
�� �ֱ��ʾ
�ֱ��ʾ ��
�� ��
��
��2���ʾ������ٴε��ͺ�������������Һ��Ũ��֮��С�� .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2011•ɽ�����ȱ�����{an}�У�a1��a2��a3�ֱ����±���һ�����������е�ijһ�����������е��κ������������±���ͬһ�У�
| | ��һ�� | �ڶ��� | ������ |
| ��һ�� | 3 | 2 | 10 |
| �ڶ��� | 6 | 4 | 14 |
| ������ | 9 | 8 | 18 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com