练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．某公司13个部门接受的快递的数量如茎叶图所示，则这13个部门接受的快递的数量的中位数为10．

    分析 利用茎图的性质和中位数的定义直接求解．

    解答 解：由茎叶图的性质得：
    某公司13个部门接受的快递的数量按从小到大的顺序排的第7个数为中位数，
    ∵第7个数是10，
    ∴这13个部门接收的快递的数量的中位数为10．
    故答案为：10．

    点评 本题考查中位数的求法，是基础题，解题时要认真审题，注意茎叶图的性质和中位数的定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．设集合M={x|x=2k+1，k∈Z}，N={x|x=k+2，k∈Z}，则．（　　）
    A．M=NB．M?NC．N?MD．M∩N=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

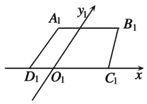    17．如图，梯形A1B1C1D1是一平面图形ABCD的直观图（斜二测），若AD∥Oy，AB∥CD，A1B1=$\frac{3}{4}{C_1}{D_1}=3，{A_1}{D_1}$=1，则原平面图形ABCD的面积是（　　）
    A．14．B．7C．$14\sqrt{2}$D．$7\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某中学有学生270人，其中一年级108人，二、三年级各81人，现要用抽样方法抽取10人组成一个样本．将学生按一、二、三年级依次同一编号为1，2，…，270．如果抽得号码有如下四种情况：
    ①5，9，100，107，111，121，180，195，200，265；
    ②7，34，61，88，115，142，169，196，223，250；
    ③30，57，84，111，138，165，192，219，246，270；
    ④11，38，60，90，119，146，173，200，227，254．
    则其中可能由分层抽样、而不可能由系统抽样得到的样本是（　　）
    A．①②B．①④C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

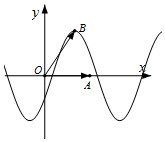    1．直角坐标系xOy中，已知点A（1，0），函数f（x）=sin（2x-$\frac{π}{6}$）的图象在y轴右侧的第一个最高点为B，则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．棱台的两底面面积为S1、S2，中截面（过各棱中点的面积）面积为S0，那么（　　）
    A．$2\sqrt{S_0}=\sqrt{S_1}+\sqrt{S_2}$B．${S_0}=\sqrt{{S_1}{S_2}}$C．2S0=S1+S2D．S02=2S1S2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点M（2，1），且离心率为$\frac{\sqrt{3}}{2}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若过原点的直线l1与椭圆C交于P，Q两点，且在直线l2：x-y+2$\sqrt{6}$=0上存在点M，使得△MPQ为等边三角形，求直线l1的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知数列{an}的前n项和${S_n}=6n-{n^2}$，则数列 $\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前20项和等于$-\frac{4}{35}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．如图所示的正四棱台的上底面边长为2，下底面边长为8，高为3$\sqrt{2}$，则它的侧棱长为6．

    查看答案和解析>>

    同步练习册答案