
【题目】已知函数f(x)=![]() x3+
x3+![]() x2+
x2+![]() x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
【答案】见解析
【解析】
解 因为f′(x)=x2+![]() x+
x+![]() =
=![]() (x+a-2),所以令f′(x)=0,
(x+a-2),所以令f′(x)=0,
解得x1=![]() ,x2=2-a.
,x2=2-a.
由0<a<1,知1<2-a<2.
所以令f′(x)>0,得x<![]() ,或x>2-a;
,或x>2-a;
令f′(x)<0,得![]() <x<2-a,
<x<2-a,
所以函数f(x)在(1,2-a)上单调递减,在(2-a,2)上单调递增.
所以函数f(x)在[1,2]上的最小值为f(2-a)=![]() (2-a)2,最大值为max{f(1),f(2)}=max
(2-a)2,最大值为max{f(1),f(2)}=max![]() .
.
因为当0<a≤![]() 时,
时,![]() -
-![]() ≥
≥![]() a;
a;
当![]() <a<1时,
<a<1时,![]() a>
a>![]() -
-![]() ,
,
由对任意x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,得2f(x)min>f(x)max(x∈[1,2]).
所以当0<a≤![]() 时,必有2×
时,必有2×![]() (2-a)2>
(2-a)2>![]() -
-![]() ,
,
结合0<a≤![]() 可解得1-
可解得1-![]() <a≤
<a≤![]() ;
;
当![]() <a<1时,必有2×
<a<1时,必有2×![]() (2-a)2>
(2-a)2>![]() a,
a,
结合![]() <a<1可解得
<a<1可解得![]() <a<2-
<a<2-![]() .
.
综上,知所求实数a的取值范围是1-![]() <a<2-
<a<2-![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155 ![]() 到195
到195![]() 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() ,并按此分组绘制如图所示的频率分布直方图,其中第六组
,并按此分组绘制如图所示的频率分布直方图,其中第六组![]() 和第七组
和第七组![]() 还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.
(1)补全频率分布直方图;
(2)根据频率分布直方图估计这50位男生身高的中位数;
(3)用分层抽样的方法在身高为![]() 内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在
内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() (
(![]() )的离心率是
)的离心率是![]() ,过点
,过点![]() (
(![]() ,
,![]() )的动直线
)的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
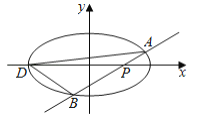
⑴求椭圆![]() 的方程:
的方程:
⑵已知![]() 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线![]() 使得
使得![]() 的面积为
的面积为![]() ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com