
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )与直线
)与直线![]() :
: ![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, ![]() ,
, ![]() 中有三个点在椭圆
中有三个点在椭圆![]() 上,剩余一个点在直线
上,剩余一个点在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() ,
, ![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)判断点![]() ,
, ![]() ,点
,点![]() 在椭圆C上,点
在椭圆C上,点![]() 在直线
在直线![]() 上,代入椭圆方程,即可求出椭圆
上,代入椭圆方程,即可求出椭圆![]() 的方程;
的方程;
(2)分类讨论,利用点差法求出直线![]() 的方程,可得直线
的方程,可得直线![]() 恒过定点.
恒过定点.
试题解析:(Ⅰ)解:由题意有3个点在椭圆C上,
根据椭圆的对称性,则点![]() ,
, ![]() 一定在椭圆C上,
一定在椭圆C上,
即![]() ,①
,①
若点![]() 在椭圆C上,
在椭圆C上,
则点![]() 必为椭圆C的左顶点,
必为椭圆C的左顶点,
而![]() ,则点
,则点![]() 一定不在椭圆C上,
一定不在椭圆C上,
故点![]() 在椭圆C上,点
在椭圆C上,点![]() 在直线l上,
在直线l上,
所以![]() ,②
,②
联立①②可解得![]() ,
, ![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)证明:由(Ⅰ)可得直线l的方程为![]() ,
,
设![]() ,
, 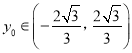 ,
,
当![]() 时,设
时,设![]() ,
, ![]() ,显然
,显然![]() ,
,
联立
则![]() ,即
,即![]() ,
,
又![]() ,即P为线段MN的中点,
,即P为线段MN的中点,
故直线MN的斜率为![]() ,
,
又![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
即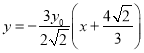 ,
,
显然![]() 恒过定点
恒过定点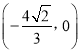 ;
;
当![]() 时,直线MN即
时,直线MN即![]() ,此时
,此时![]() 为x轴亦过点
为x轴亦过点 ,
,
综上所述, ![]() 恒过定点
恒过定点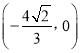 .
.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.


科目:高中数学 来源: 题型:
【题目】不等式(x+2)(x﹣1)>0的解集为( )
A.{x|x<﹣2或x>1}
B.{x|﹣2<x<1}
C.{x|x<﹣1或x>2}
D.{x|﹣1<x<2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|y=log2(x﹣1)},B={y|y=﹣x2+2x﹣2,x∈R}
(1)求集合A,B;
(2)若集合C={x|2x+a<0},且满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:分子为1且分母为正整数的分数叫做单位分数,我们可以把1拆分成多个不同的单位分数之和.例如:1= ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,1=
,1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,…,依此拆分法可得1=
,…,依此拆分法可得1= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() ,其中m,n∈N* , 则m﹣n=( )
,其中m,n∈N* , 则m﹣n=( )
A.﹣2
B.﹣4
C.﹣6
D.﹣8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知 a>0 且 a≠1,若函数f(x)=loga(x﹣1),g(x)=loga(5﹣x).
(1)求函数h(x)=f(x)﹣g(x)的定义域;
(2)讨论不等式f(x)≥g(x)成立时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,符号[x]表示不超过x的最大整数,如[2.2]=2,[﹣3.5]=﹣4,设数列{an}的通项公式为an=[log21]+[log22]+[log23]+…[log2(2n﹣1)].
(1)求a1a2a3的值;
(2)是否存在实数a,使得an=(n﹣2)2n+a(n∈N*),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣kx,x∈R(e是自然对数的底数).
(1)若k∈R,求函数f(x)的单调区间;
(2)若k>0,讨论函数f(x)在(﹣∞,4]上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下:
[60,75),2;[75,90),3;[90,105),14;[105,120),15;[120,135),12;[135,150],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在120分以上(含120分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[135,150]的学生中选两位同学,共同帮助成绩在[60,75)中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为140分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表:
分组 | 频数 | 频率 |
[60,75) | 2 | 0.04 |
[75,90) | 3 | 0.06 |
[90,105) | 14 | 0.28 |
[105,120) | 15 | 0.30 |
[120,135) | A | B |
[135,150] | 4 | 0.08 |
合计 | C | D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com