
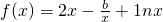 的一个极植点
的一个极植点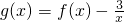 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.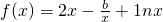 的一个极值点
的一个极值点

 ,x>0可得x>1
,x>0可得x>1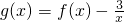 =2x+lnx
=2x+lnx )(x0-2)
)(x0-2) -2=0
-2=0 -2,则
-2,则
 可得x=2
可得x=2 )=2-ln2>0,h(2)=ln2-1<0,h(e2)=
)=2-ln2>0,h(2)=ln2-1<0,h(e2)= >0
>0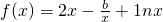 的一个极值点,可得f′(1)=0,从而可求b的值,令导数大于0,可求函数f(x)的单调增区间;
的一个极值点,可得f′(1)=0,从而可求b的值,令导数大于0,可求函数f(x)的单调增区间; -2=0,构建函数h(x)=lnx+
-2=0,构建函数h(x)=lnx+ -2,求导数,确定函数的单调性,可得h(x)与x轴有两个交点,从而可得结论.
-2,求导数,确定函数的单调性,可得h(x)与x轴有两个交点,从而可得结论.

 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源:甘肃省张掖二中2012届高三9月月考数学文科试题 题型:022
给出下列命题
(1)已知直线m,l,平面α,β,若![]() ,则
,则![]()
(2)![]() ,是
,是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
(3)如果函数y=f(x)为奇函数,则f(0)=0
(4)若![]() ,则f(x0)为极大值或极小值
,则f(x0)为极大值或极小值
(5)![]() 的图象的一个对称中心是
的图象的一个对称中心是![]()
以上命题正确的是________(注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
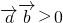 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;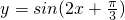 的图象的一个对称中心是
的图象的一个对称中心是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com