
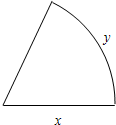
 如图,设扇形的半径为x,弧长为y.
如图,设扇形的半径为x,弧长为y.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2xy |
| S |
| S |
| S |
| S |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2x+y |
| 2 |
| P2 |
| 16 |
| P |
| 4 |
| P |
| 2 |
| P2 |
| 16 |


科目:高中数学 来源: 题型:
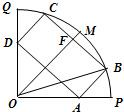 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,OB与OM之间的夹角为θ.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?
如图所示,某市政府决定在以政府大楼O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正面要朝市政府大楼.设扇形的半径OM=R,∠MOP=45°,当点B位于何处时,图书馆的占地面积最大,最大面积是多少?查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第40期 总196期 北师大课标版 题型:044
扇子在美观设计上,可以考虑用料、图案和形状,若从数学角度看,则认为符合黄金分割比例的扇子最美丽.如图,设纸扇半径为r,张开角为![]() ,要使纸扇面积与半径为r,圆心角为2π-
,要使纸扇面积与半径为r,圆心角为2π-![]() 的扇形面积的比为黄金分割比0.618,则纸扇的张开角
的扇形面积的比为黄金分割比0.618,则纸扇的张开角![]() 应为多少度?(精确到10°)
应为多少度?(精确到10°)

查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省肇庆市高一(下)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com