
(08年潮州市二模理) 我们知道:“过圆为![]() 的圆外一点
的圆外一点![]() 作它的两条切线
作它的两条切线![]() 、
、![]() ,其中
,其中![]() 、
、![]() 为切点,则
为切点,则![]() .”这个性质可以推广到所有圆锥曲线,请你写出其中一个:
.”这个性质可以推广到所有圆锥曲线,请你写出其中一个:
科目:高中数学 来源: 题型:
(08年潮州市二模理)(14分)已知函数![]() 的导数
的导数![]() 满足
满足![]() ,常数
,常数![]() 为方程
为方程![]() 的实数根.
的实数根.
⑴ 若函数![]() 的定义域为I,对任意
的定义域为I,对任意![]() ,存在
,存在![]() ,使等式
,使等式![]() =
=![]() 成立,
成立,
求证:方程![]() 不存在异于
不存在异于![]() 的实数根;
的实数根;
⑵ 求证:当![]() 时,总有
时,总有![]() 成立;
成立;
⑶ 对任意![]() ,若满足
,若满足![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
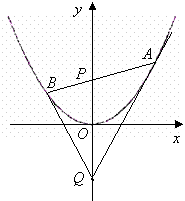
(08年潮州市二模理)(14分)如图,过抛物线![]() 的对称轴上任一点
的对称轴上任一点![]() 作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点.
⑴ 设点P满足![]() (
(![]() 为实数),证明:
为实数),证明:![]() ;
;
⑵ 设直线AB的方程是![]() ,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年潮州市二模理)(14分)
如图,四面体ABCD中,O、E分别是BD、BC的中点, ![]()
⑴ 求证:![]() 平面BCD;
平面BCD;
⑵ 求异面直线AB与CD所成角余弦的大小;
⑶ 求点E到平面ACD的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com