
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)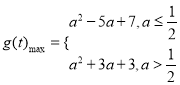
【解析】
试题(1)设二次函数一般式,根据待定系数法求出a,b,c(2)不等式恒成立一般转化为对应函数最值:x2-3x+1的最小值>m,再根据二次函数性质求x2-3x+1的最小值得实数m的范围;(3)根据对称轴与定义区间位置关系,分类讨论函数取最大值的情况
试题解析:解:(1)令f(x)=ax2+bx+c(a≠0),代入已知条件,
得:![]()
∴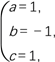
∴f(x)=x2-x+1.
(2)当x∈[-1,1]时,f(x)>2x+m恒成立,
即x2-3x+1>m恒成立;
令g(x)=x2-3x+1=![]() 2-
2-![]() ,x∈[-1,1].
,x∈[-1,1].
则对称轴:x=![]() [-1,1],g(x)min=g(1)=-1,
[-1,1],g(x)min=g(1)=-1,
∴m<-1.
(3)G(t)=f(2t+a)=4t2+(4a-2)t+a2-a+1,t∈[-1,1],对称轴为:t=![]() .
.
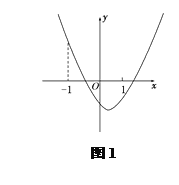
①当![]() ≥0时,即:a≤
≥0时,即:a≤![]() ;如图1:
;如图1:
G(t)max=G(-1)=4-(4a-2)+a2-a+1=a2-5a+7,
②当![]() <0时,
<0时,
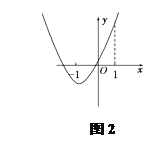 即:a>
即:a>![]() ;如图2:
;如图2:
G(t)max=G(1)=4+(4a-2)+a2-a+1=a2+3a+3,
综上所述:
G(t)max=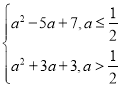


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为
(a>b>0)的左焦点F1与抛物线y2=﹣4x的焦点重合,椭圆E的离心率为 ![]() ,过点M (m,0)(m>
,过点M (m,0)(m> ![]() )作斜率不为0的直线l,交椭圆E于A,B两点,点P(
)作斜率不为0的直线l,交椭圆E于A,B两点,点P( ![]() ,0),且
,0),且 ![]() 为定值.
为定值.
(Ⅰ)求椭圆E的方程;
(Ⅱ)求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为二次函数,且f(x-1)+f(x)=2x2+4.
(1)求f(x)的解析式;
(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
(1)求抛物线C的方程及准线l的方程;
(2)过焦点F的直线(不经过Q点)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1 , k2 , k3 , 问是否存在常数λ,使得k1+k2=λk3成立?若存在λ,求出λ的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①已知X服从正态分布N(0,σ2),且P(﹣2≤X≤2)=0.6,则P(X>2)=0.2;
②若命题 ![]() ,则¬p:x∈(﹣∞,1),x2﹣x﹣1≥0;
,则¬p:x∈(﹣∞,1),x2﹣x﹣1≥0;
③已知直线l1:ax+3y﹣1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 ![]() .
.
其中正确的结论的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过5千元).已知加工此农产品还要投入成本
(其中推广促销费不能超过5千元).已知加工此农产品还要投入成本![]() 万元(不包括推广促销费用),若加工后的每件成品的销售价格定为
万元(不包括推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润=销售额-成本-推广促销费)
万元的函数;(利润=销售额-成本-推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com