Question

计算：cos²75°+cos²15°+cos75°cos15°．

Answer 1

【答案】分析：利用两角和差的余弦公式，以及诱导公式，求出cos75°和cos15°的值，代入要求的式子化简即得所求．
解答：解：cos75°=cos（45°+30°）=cos45°cos30°-sin45°sin30°=．
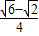
cos15°=cos（45°-30°）=cos45°cos30°+sin45°sin30°=．
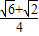
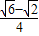
cos²75°+cos²15°+cos75°cos15°=cos²75°+sin²75°+•=1+=．
点评：本题考查两角和差的余弦公式，同角三角函数的基本关系，以及诱导公式的应用，求出cos75°和cos15°的值，
是解题的关键．