
已知函数 满足:对任意
满足:对任意 ,
,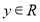 ,都有
,都有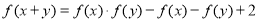 成立,且
成立,且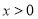 时,
时, .
.
(1)求 的值,并证明:当
的值,并证明:当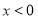 时,
时,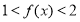 ;
;
(2)判断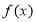 的单调性并加以证明;
的单调性并加以证明;
(3)若函数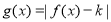 在
在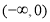 上递减,求实数
上递减,求实数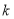 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届福建连城县朋口中学高三上期中数学(文)试卷(解析版) 题型:选择题
给出下列命题:①存在实数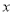 ,使
,使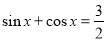 ;②若
;②若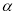 ,
,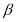 是第一象限角,且
是第一象限角,且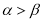 ,则
,则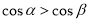 ;③函数
;③函数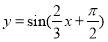 是偶函数;④函数
是偶函数;④函数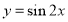 的图象向左平移
的图象向左平移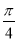 个单位,得到函数
个单位,得到函数 的图象.
的图象.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2017届福建连城县朋口中学高三上期中数学(理)试卷(解析版) 题型:解答题
在△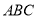 中,
中,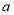 ,
,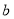 ,
,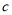 分别为角
分别为角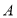 ,
,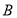 ,
,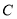 所对的三边,
所对的三边,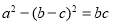 .
.
(1)求角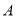 ;
;
(2)若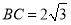 ,角
,角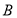 等于
等于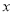 ,周长为
,周长为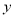 ,求函数
,求函数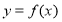 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届福建连城县朋口中学高三上期中数学(理)试卷(解析版) 题型:选择题
设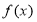 是定义在
是定义在 上的偶函数,它在
上的偶函数,它在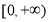 上为增函数,且
上为增函数,且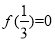 ,则不等式
,则不等式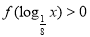 的解集为( )
的解集为( )
A.
B.
C.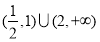
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北唐山市高一上期中数学试卷(解析版) 题型:填空题
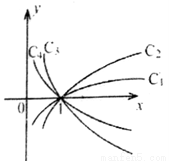
欧巴老师布置给时镇同学这样一份数学作业:在同一个直角坐标系中画出四个对数函数的图象,使它们的底数分别为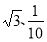 和
和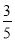 .时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为
.时镇同学为了和暮烟同学出去玩,问大英同学借了作业本很快就抄好了,详见如图.第二天,欧巴老师当堂质问时镇同学:“你画的四条曲线中,哪条是底数为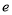 的对数函数图象?” 时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线 才是底数为
的对数函数图象?” 时镇同学无言以对,憋得满脸通红,眼看时镇同学就要被欧巴老师训斥一番,聪明睿智的你能不能帮他一把,回答这个问题呢?曲线 才是底数为 的对数函数的图象.
的对数函数的图象.
查看答案和解析>>
科目:高中数学 来源:2017届湖北荆荆襄宜四地七校联盟高三文上联考一数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求函数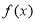 的单调区间;
的单调区间;
(2)若方程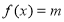
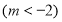 有两个相异实根
有两个相异实根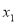 ,
, ,且
,且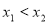 ,证明:
,证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com