
分析 (Ⅰ)通过设P(x,y)、动圆P的比较为r,利用圆与圆的位置关系可知|PF1|=1+r、|PF2|=5-r,进而化简可知动圆圆心P的轨迹是以F1(-1,0)、F2(1,0)为焦点、长轴长为6的椭圆,计算即得结论;
(Ⅱ)通过(I)可知A1(-3,0)、A2(3,0),通过设M(x,y),利用$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=及k1k2=$\frac{y-0}{x+3}$•$\frac{y-0}{x-3}$化简计算即得结论;
(Ⅲ)通过设过点(2,0)的直线l方程为x=my+2,并与曲线C方程联立,利用韦达定理及N(x1+x2,y1+y2)在曲线C上化简计算即得结论.
解答 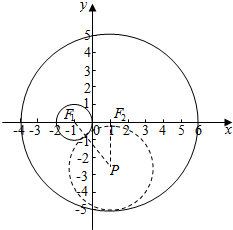 解:(Ⅰ)依题意,F1(-1,0),F2(1,0),
解:(Ⅰ)依题意,F1(-1,0),F2(1,0),
设P(x,y),动圆P的比较为r,则|PF1|=1+r,|PF2|=5-r,
∴|PF1|+|PF2|=6,
∴动圆圆心P的轨迹是以F1(-1,0)、F2(1,0)为焦点,长轴长为6的椭圆,
则b2=a2-c2=9-1=8,
于是曲线C的方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1;
(Ⅱ)由(I)可知A1(-3,0),A2(3,0),
设M(x,y),则$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1,
于是k1k2=$\frac{y-0}{x+3}$•$\frac{y-0}{x-3}$=$\frac{{y}^{2}}{{x}^{2}-9}$=$\frac{{y}^{2}}{-\frac{9{y}^{2}}{8}}$=-$\frac{8}{9}$;
(Ⅲ)结论:在曲线C上存在点N,使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$,且直线l方程为x=±$\frac{\sqrt{14}}{4}$y+2.
理由如下:
设过点(2,0)的直线l方程为:x=my+2,
联立直线l与曲线C的方程,消去x,整理得:
(9+8m2)y2+32my-40=0,
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{32m}{9+8{m}^{2}}$,y1y2=-$\frac{40}{9+8{m}^{2}}$,
∵$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$,
∴N(x1+x2,y1+y2)在曲线C上,
∴$\frac{({x}_{1}+{x}_{2})^{2}}{9}$+$\frac{({{y}_{1}+{y}_{2})}^{2}}{8}$=1,
又∵x1+x2=m(y1+y2)+4=4-$\frac{32{m}^{2}}{9+8{m}^{2}}$=$\frac{36}{9+8{m}^{2}}$,
∴$\frac{1}{9}$•$(\frac{36}{9+8{m}^{2}})^{2}$+$\frac{1}{8}$•$(-\frac{32m}{9+8{m}^{2}})^{2}$=1,
整理得:9+8m2=16,
解得:m=±$\frac{\sqrt{14}}{4}$,
于是在曲线C上存在点N,使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$,且直线l方程为x=±$\frac{\sqrt{14}}{4}$y+2.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2 | B. | y=x-2 | C. | $y={(\frac{1}{4})^{-|x|}}$ | D. | $y={log_3}{x^{\frac{5}{6}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com