
【题目】如图所示,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,且满足![]() .
.

(1)求证:四边形EFGH是梯形;
(2)若BD=a,求梯形EFGH的中位线的长.
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
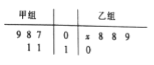
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙依次有放回地随机抽取1个小球,取到小球的编号分别为![]() .在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
.在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆因夏长酷热多伏旱而得名“火炉”,八月是重庆最热、用电量最高的月份.下图是沙坪坝区居民八月份用电量(单位:度)的频率分布直方图,其分组区间依次为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中的![]() ;
;
(2)根据直方图估计八月份用电量的众数和中位数;
(3)在用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则用电量在![]() 的用户应抽取多少户?
的用户应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图. 为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求a>b的概率;
(3)若a=1,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断b为何值时,
,根据茎叶图推断b为何值时,![]() 达到最值.
达到最值.
(只需写出结论)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]()
给出下列结论:
①四面体![]() 每个面的面积相等;
每个面的面积相等;
②从四面体![]() 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
③连结四面体![]() 每组对棱中点的线段相互垂直平分;
每组对棱中点的线段相互垂直平分;
④从四面体![]() 每个顶点出发的三条棱的长可作为一个三角形的三边长;
每个顶点出发的三条棱的长可作为一个三角形的三边长;
其中正确结论的序号是__________。(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com