
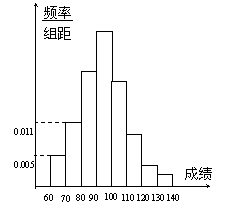
 为了解某次测验成绩,在全年级随机地抽查了100名学生的成绩,得到频率分布直方图(如图),由于某种原因使部分数据丢失,但知道后5组的学生人数成等比数列,设90分以下人数为38,最大频率为b,则b的值为
为了解某次测验成绩,在全年级随机地抽查了100名学生的成绩,得到频率分布直方图(如图),由于某种原因使部分数据丢失,但知道后5组的学生人数成等比数列,设90分以下人数为38,最大频率为b,则b的值为| 1 |
| q |
| a(1-q5) |
| 1-q |
| 1 |
| q |
| 1 |
| 2 |
| a |
| 100 |
| 1 |
| q |


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
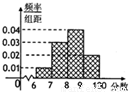
 (2013•烟台二模)某校高三年级的学生共1000人,一次测验成绩的分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取50人了解情况,则在80~90分数段应抽取人数为
(2013•烟台二模)某校高三年级的学生共1000人,一次测验成绩的分布直方图如图所示,现要按如图所示的4个分数段进行分层抽样,抽取50人了解情况,则在80~90分数段应抽取人数为查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西师大附中高二(上)期中数学试卷(文科)(解析版) 题型:填空题

查看答案和解析>>
科目:高中数学 来源:2013年山东省烟台市高考数学二模试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年重庆一中一模文)为了解某次测验成绩,在全年级随机地抽查了100名学生的成绩,得到频率分布直方图(如右图),由于某种原因使部分数据丢失,但知道后5组的学生人数成等比数列,设90分以下人数为![]() ,最大频率为
,最大频率为![]() ,则
,则![]() 的值分别为( )
的值分别为( )
A.69, 0.53 B.38, 0.32
C.69, 5.3 D.38, 3.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com