Question

在正方体ABCD—A₁B₁C₁D₁中,求以下各对异面直线所成的角:

(1)AB、CC₁;(2)AB₁、CD₁;

(3)AB₁、CD;(4)AB₁、BC₁.

Answer 1

解析:(1)∵ABCD—A₁B₁C₁D₁为正方体,

             ①

∴BB₁与CC₁平行,∴AB与BB₁所成的锐角或直角就是AB与CC₁所成的角.

又∵AB与BB₁所成的角为直角,故AB与CC₁所成的角为直角,即为90°,如图①.

(2)如图②,连结A₁B,

由ABCD—A₁B₁C₁D₁为正方体可得A₁D₁∥AD,BC∥AD,

            ②

故有A₁D₁∥BC,

∴四边形A₁D₁CB是平行四边形.

∴A₁B∥CD₁.

因此,AB₁与A₁B所成的锐角或直角就是AB₁、CD₁所成的角.

由正方形的性质可知AB₁与A₁B所成的角为直角,

∴AB₁、CD₁所成的角为直角,即为90°.

(3)如图③,由AB与CD平行可得AB₁与CD所成的角就是∠B₁AB,而由正方形的性质可知这个角为45°.

               ③

∴AB₁与CD所成的角为45°.

(4)如图④,连结AD₁,如前所述可知AB与C₁D₁平行且相等,进而可知四边形ABC₁D₁为平行四边形,

∴AD₁与BC₁平行且相等,由此可知∠D₁AB₁即是所求的两条异面直线所成的角或其补角(现在还不知道这个角的大小).连结B₁D₁,

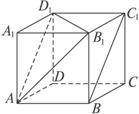
              ④

在△D₁AB₁中,AB₁=B₁D₁=AD₁(都是边长相等的正方形的对角线),

由此我们可知△D₁AB₁是正三角形,

∴∠D₁AB₁的大小为60°.

小结:(1)在求两条异面直线所成的角时,应注意充分利用题中现有的线段,在很多情况下,已知条件中已经存在与两条异面直线平行的线段,只需我们把它找到即可.

(2)在作两条异面直线的平行线时,我们通常采用平移的办法来解决,比如这个问题中,我们可以想象把线段CD₁平移到A₁B,这种方法看起来与作平行的效果是相同的,但实际应用中是非常简捷方便的.以后我们在解题的过程中一般都采用平移的方法来解决这个问题.

(3)在研究此类问题时,我们首先要把研究的对象(两条异面直线)通过平移的方法使它们成为两条相交直线.

(4)求两条异面直线所成的角,主要的问题是平移,找平行线,如果没有思路,我们可以试着把其中的一个线段平移,也可把两个线段都平移而得到两条相交直线.但是不管怎样平移,中心目标是能够形成一个可解的三角形.