Question

形如

a b c d

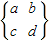的式子叫做二行二列矩阵，定义矩阵的一种运算

a b c d

•

x y

=

ax+bx cx+dy

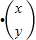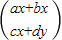．该运算的几何意义为平面上的点（x，y）在矩阵

a b c d

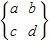的作用下变换成点（ax+by，cx+dy）．
（1）设点M（-2，1）在

0 1 1 0

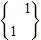的作用下变换成点M′，求点M′的坐标；
（2）设数列{a_n} 的前n项和为S_n ，且对任意正整数n，点A（S_n，n）在

0 1 1 0

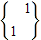的作用下变换成的点A′在函数f（x）=x²+x的图象上，求a_n的表达式；
（3）在（2）的条件下，设b_n为数列{1-

1

an

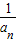}的前n项的积，是否存在实数a使得不等式bn

an+1

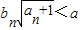＜a对一切n∈N^*都成立？若存在，求a的取值范围；若不存在，请说明理由．

Answer 1

（1）∵

0 1 1 0

-2 1

=

1 -2

∴点M′的坐标为（1，-2）；
（2）∵

0 1 1 0

Sn n

=

n Sn

，∴A′（n，S_n）
∵点A′（n，S_n）在函数f（x）=x²+x的图象上，∴S_n=n²+n
当n=1时，a₁=S₁=2
当n≥2时，a_n=S_n-S_n-1=2n
a₁=2满足上式，∴a_n=2nn∈N^*
（3）bn=(1-

1

a1

)(1-

1

a2

)(1-

1

an

)，设Fn=(1-

1

a1

)(1-

1

a2

)(1-

1

an

)

2n+1

∵

F(n+1)

F(N)

=

2n+1 • 2n+3

2n+2

＜1
∴F（n）＞F（n+1），F（n）单调递减．
∴当n=1时，F（n）取最大值

3

2

要使不等式bn

an+1

＜a对一切n∈N^*都成立，只需a＞

3

2

所以a的取值范围为(

3

2

，+∞)