
【题目】已知椭圆![]() :
:![]() , 过点
, 过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于M、N两点(M点在N点的上方),与
交于M、N两点(M点在N点的上方),与![]() 轴交于点E.
轴交于点E.
(1)当![]() 且
且![]() 时,求点M、N的坐标;
时,求点M、N的坐标;
(2)当![]() 时,设
时,设![]() ,
,![]() ,求证:
,求证:![]() 为定值,并求出该值;
为定值,并求出该值;
(3)当![]() 时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于
时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)M(0,1),N (![]() ,
,![]() );(2)
);(2)![]() 为定值3(3)
为定值3(3)![]()
【解析】
(1)代值联立方程组.解得即可求出,
(2)联立方程,利用韦达定理,以及向量的知识可得从而![]() ,化简整理即可证明,
,化简整理即可证明,
(3)假设存在直线l:y=k(x+1)满足题意,则△MNF的内切圆的半径为![]() ,根据韦达定理,弦长公式,三角形的面积公式,即可求出k的值
,根据韦达定理,弦长公式,三角形的面积公式,即可求出k的值
解:(1) 当m=k=1时,联立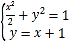 ,解之得:
,解之得:![]() 或
或 ,
,
即M(0,1),N (![]() ,
,![]() );
);
(2) 当m=2时联立 ,消去y得:
,消去y得:![]() ,
,
设M(x1,y1),N (x2,y2),则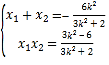 ,
,
由![]() ,
,![]() ,且点
,且点![]() 的横坐标为0,
的横坐标为0,
得![]() 、
、![]() . 从而
. 从而![]()
![]() =
=![]()
=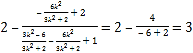 ,
,
![]() 为定值3;
为定值3;
(3) 当m=3时,椭圆![]() :
:![]() ,假设存在直线
,假设存在直线![]() 满足题意,则△
满足题意,则△![]() 的内切圆的半径为
的内切圆的半径为![]() ,又
,又![]() 、
、![]() 为椭圆
为椭圆![]() 的焦点,故△MNF的周长为8,
的焦点,故△MNF的周长为8,
从而![]() ,
,
消去![]() ,得
,得![]() ,设
,设![]() 、
、![]() ,
,
则![]() .
.
故![]() ,即
,即![]() .
.
由(2),得 ,
,
化简,得![]() ,解得
,解得![]() ,
,
故存在直线![]() 满足题意.
满足题意.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再将所有点的横坐标缩短到原来的
个单位,再将所有点的横坐标缩短到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像则下面对函数
的图像则下面对函数![]() 的叙述不正确的是( )
的叙述不正确的是( )
A.函数![]() 的周期
的周期![]()
B.函数![]() 的一个对称中心
的一个对称中心![]()
C.函数![]() 在区间
在区间![]() 内单调递增
内单调递增
D.当![]() ,
,![]() 时,函数
时,函数![]() 有最小值
有最小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队员进行定点投篮训练,每次投中的概率是![]() ,且每次投篮的结果互不影响.
,且每次投篮的结果互不影响.
(1)假设这名队员投篮5次,求恰有2次投中的概率;
(2)假设这名队员投篮3次,每次投篮,投中得1分,为投中得0分,在3次投篮中,若有2次连续投中,而另外一次未投中,则额外加1分;若3次全投中,则额外加3分,记![]() 为队员投篮3次后的总的分数,求
为队员投篮3次后的总的分数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
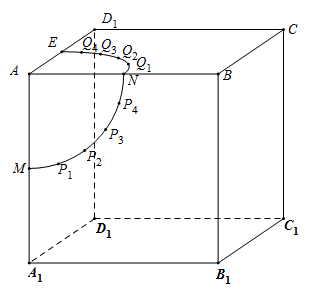
【题目】如图,棱长为2的正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() 的中点,以
的中点,以![]() 为圆心,1为半径,分别在面
为圆心,1为半径,分别在面![]() 和面
和面![]() 内作弧
内作弧![]() 和
和![]() ,并将两弧各五等分,分点依次为
,并将两弧各五等分,分点依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只蚂蚁欲从点
.一只蚂蚁欲从点![]() 出发,沿正方体的表面爬行至
出发,沿正方体的表面爬行至![]() ,则其爬行的最短距离为________.参考数据:
,则其爬行的最短距离为________.参考数据:![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对边分别为a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC边上的中线SD的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com