
【题目】已知函数 f(x)=2lnx+x2﹣ax. (Ⅰ)当a=5时,求f(x)的单调区间;
(Ⅱ)设A(x1 , y1),B(x2 , y2)是曲线y=f(x)图象上的两个相异的点,若直线AB的斜率k>1恒成立,求实数a的取值范围;
(Ⅲ)设函数f(x)有两个极值点x1 , x2 , x1<x2且x2>e,若f(x1)﹣f(x2)≥m恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)当a=5时,f(x)=2lnx+x2﹣5x.求导,
f′(x)= ![]() =
= ![]() ,(x>0),
,(x>0),
令f′(x)>0,解得:x>2或0<x< ![]() ,
,
令f′(x)<0,解得: ![]() <x<2,
<x<2,
∴f(x)的单调递增区间(0, ![]() ),(2,+∞);f(x)的单调递减区间(
),(2,+∞);f(x)的单调递减区间( ![]() ,2);
,2);
(Ⅱ)由题意可知:k= ![]() >1,∴
>1,∴ 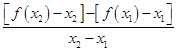 >0,
>0,
令g(x)=f(x)﹣x,则g(x)在(0,+∞)上单调递增,
∴g′(x)=f′(x)﹣1≥0,
∴ ![]() ﹣1≥0在(0,+∞)上恒成立,
﹣1≥0在(0,+∞)上恒成立,
∴a≤2x+ ![]() ﹣1在(0,+∞)上恒成立,
﹣1在(0,+∞)上恒成立,
∵2x+ ![]() ≥4,x=1时取等号,
≥4,x=1时取等号,
∴a≤3;
(Ⅲ)∵x1+x2= ![]() ,x1x2=1,∴a=2(x1+x2),x2=
,x1x2=1,∴a=2(x1+x2),x2= ![]() ,
,
∴f(x1)﹣f(x2)=(2lnx1+x12﹣ax1)﹣(2lnx2+x22﹣ax2)= ![]() ﹣x12+2lnx12,
﹣x12+2lnx12,
令x12=x,则0<x< ![]() ,g(x)=
,g(x)= ![]() ﹣x﹣2lnx,
﹣x﹣2lnx,
∴g′(x)=﹣ ![]() <0,
<0,
∴g(x)在(0, ![]() )上单调递减,
)上单调递减,
∴g(x)>g( ![]() )=
)= ![]() ﹣4,
﹣4,
∴m≤ ![]() ﹣4.
﹣4.
【解析】(Ⅰ)当a=5时,f(x)=2lnx+x2﹣5x.求导,利用导数的正负求f(x)的单调区间;(Ⅱ)由题意可知:k= ![]() >1,
>1, ![]() >0,构造函数,确定函数的单调性,分离参数,即可求实数a的取值范围;(Ⅲ)f(x1)﹣f(x2)=(2lnx1+x12﹣ax1)﹣(2lnx2+x22﹣ax2)=
>0,构造函数,确定函数的单调性,分离参数,即可求实数a的取值范围;(Ⅲ)f(x1)﹣f(x2)=(2lnx1+x12﹣ax1)﹣(2lnx2+x22﹣ax2)= ![]() ﹣x12+2lnx12,令x12=x,则0<x<
﹣x12+2lnx12,令x12=x,则0<x< ![]() ,g(x)=
,g(x)= ![]() ﹣x﹣2lnx,求导,确定函数的单调性,求最值,即可求实数m的取值范围.
﹣x﹣2lnx,求导,确定函数的单调性,求最值,即可求实数m的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为 ![]() 的等边三角形,直线MF的倾斜角为60°.
的等边三角形,直线MF的倾斜角为60°.
(1)求抛物线E的方程;
(2)如图,直线m过点F交抛物线E于C、D两点,Q(2,0),直线CQ、DQ分别交抛物线E于G、H两点,设直线CD、GH的斜率分别为k1、k2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法: ①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(﹣1<X<0)= ![]() ﹣p
﹣p
④回归直线一定过样本点的中心( ![]() ,
, ![]() ).
).
其中正确的说法有(请将你认为正确的说法的序号全部填写在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记U={1,2,…,100},对数列{an}(n∈N*)和U的子集T,若T=,定义ST=0;若T={t1 , t2 , …,tk},定义ST= ![]() +
+ ![]() +…+
+…+ ![]() .例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
.例如:T={1,3,66}时,ST=a1+a3+a66 . 现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.
(1)求数列{an}的通项公式;
(2)对任意正整数k(1≤k≤100),若T{1,2,…,k},求证:ST<ak+1;
(3)设CU,DU,SC≥SD , 求证:SC+SC∩D≥2SD .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,f′(x)为函数f(x)的导函数,当x∈[0.+∞)时,2sinxcosx﹣f′(x)>0且x∈R,f(﹣x)+f(x)+cos2x=1.则下列说法一定正确的是( )
A.![]() ﹣f(﹣
﹣f(﹣ ![]() )>
)> ![]() ﹣f(﹣
﹣f(﹣ ![]() )
)
B.![]() ﹣f(﹣
﹣f(﹣ ![]() )>
)> ![]() ﹣f(﹣
﹣f(﹣ ![]() )
)
C.![]() ﹣f(
﹣f( ![]() )>
)> ![]() ﹣f(
﹣f( ![]() )
)
D.![]() ﹣f(﹣
﹣f(﹣ ![]() )>
)> ![]() ﹣f(
﹣f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x﹣b)(b∈R).若存在x∈[ ![]() ,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
,2],使得f(x)+xf′(x)>0,则实数b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a∈R,集合A={x|(x﹣1)(x﹣a)≥0},B={x|x≥a﹣1},若A∪B=R,则a的取值范围为( )
A.(﹣∞,2)
B.(﹣∞,2]
C.(2,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标. 某市环保局从市区2016年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(Ⅱ)从这15天的数据中任取3天的数据,记ξ表示其中空气质量达到一级的天数,求ξ的分布列;
(Ⅲ)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com