
【题目】如图,两座建筑物![]() 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9![]() 和15
和15![]() ,从建筑物
,从建筑物![]() 的顶部
的顶部![]() 看建筑物
看建筑物![]() 的视角
的视角![]() .
.

(1)求![]() 的长度;
的长度;
(2)在线段![]() 上取一点
上取一点![]() 点
点![]() 与点
与点![]() 不重合),从点
不重合),从点![]() 看这两座建筑物的视角分别为
看这两座建筑物的视角分别为![]() 问点
问点![]() 在何处时,
在何处时,![]() 最小?
最小?
【答案】(1)18 (2)当![]() 为
为![]() 时,
时,![]() 取得最小值
取得最小值
【解析】
试题(1)作![]()
![]() ,垂足为
,垂足为![]() ,在已知三角形ACD中将所求的BC边与已知的AB,CD用三角形内角
,在已知三角形ACD中将所求的BC边与已知的AB,CD用三角形内角![]() 的三角函数值联系起来,得到所求边的方程,从而求解边长值;(2)求角的大小一般转化为先求角的三角函数值的大小,借助于得到的BC边长将两角的正切值用已知三边表示即得到了角与边长的三角函数关系,从而转化为求函数值域问题,当函数式较复杂时可考虑函数导数工具求值域
的三角函数值联系起来,得到所求边的方程,从而求解边长值;(2)求角的大小一般转化为先求角的三角函数值的大小,借助于得到的BC边长将两角的正切值用已知三边表示即得到了角与边长的三角函数关系,从而转化为求函数值域问题,当函数式较复杂时可考虑函数导数工具求值域
试题解析:(1)作![]()
![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,![]() ,设
,设![]() ,
,
则![]()
 ,化简得
,化简得![]() ,解之得,
,解之得,![]() 或
或![]() (舍)
(舍)
答:![]() 的长度为
的长度为![]() .
.
(2)设![]() ,则
,则![]() ,
,
 .
.
设![]() ,
,![]() ,令
,令![]() ,因为
,因为![]() ,得
,得![]() ,当
,当
![]() 时,
时,![]() ,
,![]() 是减函数;当
是减函数;当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
所以,当![]() 时,
时,![]() 取得最小值,即
取得最小值,即![]() 取得最小值,12分
取得最小值,12分
因为![]() 恒成立,所以
恒成立,所以![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() 在
在![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() 取得最小值.
取得最小值.
答:当![]() 为
为![]() 时,
时,![]() 取得最小值.
取得最小值.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:高中数学 来源: 题型:
【题目】某地级市共有![]() 中学生,其中有
中学生,其中有![]() 学生在
学生在![]() 年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为
年享受了“国家精准扶贫”政策,在享受“国家精准扶贫”政策的学生中困难程度分为三个等次:一般困难、很困难、特别困难,且人数之比为![]() ,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助
,为进一步帮助这些学生,当地市政府设立“专项教育基金”,对这三个等次的困难学生每年每人分别补助![]() 元、
元、![]() 元、
元、![]() 元.经济学家调查发现,当地人均可支配年收入较上一年每增加
元.经济学家调查发现,当地人均可支配年收入较上一年每增加![]() ,一般困难的学生中有
,一般困难的学生中有![]() 会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生有
会脱贫,脱贫后将不再享受“精准扶贫”政策,很困难的学生有![]() 转为一般困难学生,特别困难的学生中有
转为一般困难学生,特别困难的学生中有![]() 转为很困难学生.现统计了该地级市
转为很困难学生.现统计了该地级市![]() 年到
年到![]() 年共
年共![]() 年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份
年的人均可支配年收入,对数据初步处理后得到了如图所示的散点图和表中统计量的值,其中年份![]() 取
取![]() 时代表
时代表![]() 年,
年,![]() 取
取![]() 时代表
时代表![]() 年,……依此类推,且
年,……依此类推,且![]() 与
与![]() (单位:万元)近似满足关系式
(单位:万元)近似满足关系式![]() .(
.(![]() 年至
年至![]() 年该市中学生人数大致保持不变)
年该市中学生人数大致保持不变)
|
|
|
|
|
|

(1)估计该市![]() 年人均可支配年收入为多少万元?
年人均可支配年收入为多少万元?
(2)试问该市![]() 年的“专项教育基金”的财政预算大约为多少万元?
年的“专项教育基金”的财政预算大约为多少万元?
附:对于一组具有线性相关关系的数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厦门市从2003年起每年都举行国际马拉松比赛,每年马拉松比赛期间,都会吸引许多外地游客到厦门旅游,这将极大地推进厦门旅游业的发展,旅游部门将近六年马拉松比赛期间外地游客数量统计如下表:
年份 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
比赛年份编号 |
|
|
|
|
|
|
外地游客人数 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;(精确到
的线性回归方程;(精确到![]() )
)
(2)若用对数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,且相关指数
,且相关指数![]() ,请用相关指数说明选择哪个模型更合适.(精确到
,请用相关指数说明选择哪个模型更合适.(精确到![]() )
)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
参考公式:回归方程![]() 中,
中, ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区![]() 年至
年至![]() 年农村居民家庭人均纯收入
年农村居民家庭人均纯收入![]() (单位:千元)的数据如表:
(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析![]() 年至
年至![]() 年该地区农村居民家庭人纯收入的变化情况,并预测该地区
年该地区农村居民家庭人纯收入的变化情况,并预测该地区![]() 年农村居民家庭人均纯收入.
年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数f(x)=(ex﹣1)(x﹣1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取得极小值
B.当k=1时,f(x)在x=1处取得极大值
C.当k=2时,f(x)在x=1处取得极小值
D.当k=2时,f(x)在x=1处取得极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算).有人独立来该租车点则车骑游.各租一车一次.设甲、乙不超过两小时还车的概率分别为![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(Ⅰ)求出甲、乙所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() +
+ ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D. 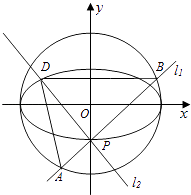
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P1 , P2 , …Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1 , P2 , …Pn的距离之和最小,则称点P为P1 , P2 , …Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点,现有下列命题:
①若三个点A、B、C共线,C在线段AB上,则C是A,B,C的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A、B、C、D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是(写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com