
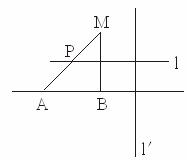
(1)求证:点P到点B的距离与到直线l′的距离之比为定值.
(2)若P点到A、B两点的距离之积为m,当m取最大值时,求P点的坐标.
(3)设直线y=kx+m(k≠0)与点P所在曲线相交于不同两点C、D,定点G(0,-![]() ),则使|GC|=|GD|的正数m是否存在?若存在,则求出其取值范围;若不存在,请说明理由.
),则使|GC|=|GD|的正数m是否存在?若存在,则求出其取值范围;若不存在,请说明理由.
(1)证明:A(-2,0),B(2,0), l′:x=![]() .
.
由题意,|PA|+|PM|=|PA|+|PB|=6且|AB|=4.
∴点P在椭圆![]() =1上.
=1上.
∴l′:x=![]() 为椭圆的右准线,且右焦点为B(2,0),若P到l′的距离为d,则
为椭圆的右准线,且右焦点为B(2,0),若P到l′的距离为d,则![]() =e=
=e=![]() 为定值.
为定值.
(2)解:m=|PA|·|PB|=(![]() )2=9.
)2=9.
当|PA|=|PB|,即P(0,-![]() )或(0,
)或(0,![]() )时m取最大值.
)时m取最大值.
(3)解:设存在直线y=kx+m(k≠0)与P点所在曲线交于C(x1,y1)、D(x2,y2)两点,CD中点为N(x0,y0),
则x0=![]() ,|GC|=|GD|,
,|GC|=|GD|,
即GN为CD的中垂线,kCD·kGN=k·kGN=-1.
由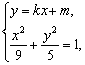
得(5+9k2)x2+18mkx+
x1+x2=-![]() .
.
由Δ>0得9k2+5>m2. ![]() ①
①
又x0=![]() =-
=-![]() ,
,
y0=kx0+m=![]() ,
,
kGN=-![]() =-
=-![]() .
.
∴5![]() +
+![]() k2=
k2=
由①②得![]() (9k2+5)=
(9k2+5)=![]() m2.
m2.
∴0<m<![]()
![]() .
.
但由②9![]() k2=
k2=![]() >0得m>
>0得m>![]() ,二者矛盾,故这样的正数m不存在.
,二者矛盾,故这样的正数m不存在.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:2012-2013学年河北省石家庄市高三下学期第二次质量检测理科数学试卷(解析版) 题型:选择题
下图是两个全等的正三角形.给定下列三个命题:①存在四 棱锥,其正视图、侧视图如右图;②存在三棱锥,其正视图、侧视图如右图;③存在圆锥,其正视图、侧视图如右图.其中 真命题的个数是
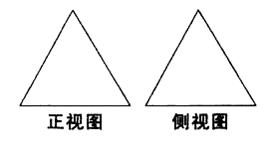
A.3 B.2 C.1 D.O
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌市高三第二次模拟测试理科数学试卷(解析版) 题型:选择题
下图展示了一个由区间(―π,π)到实数集R的映射过程:区间(―π,π)中的实数x对应轴上的点M(如图1):将线段AB围成一个圆,使两端点A、B恰好重合(从A到B是逆时针,如图2):再将这个圆放在平面直角坐标系中,使其圆心在x轴上,点A的坐标为(1,0)(如图3),图3中直线OM的斜率为k,则x的象就是k,记作k=¦(x).有下列判断(1)¦(x)是奇函数;(2) ¦(x)是存在3个极值点的函数;(3) ¦(x)的值域是[―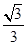 ,
,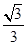 ];
];
(4) ¦(x)是区间(―π,π)上的增函数。其中正确的是
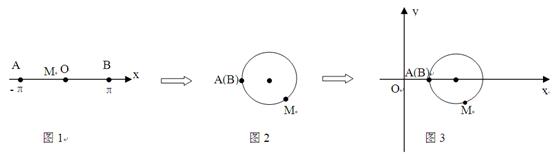
A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com